Google CTF Quals 2019 - Flaggy Bird
Challenge overwiew
An Android APK challenge.
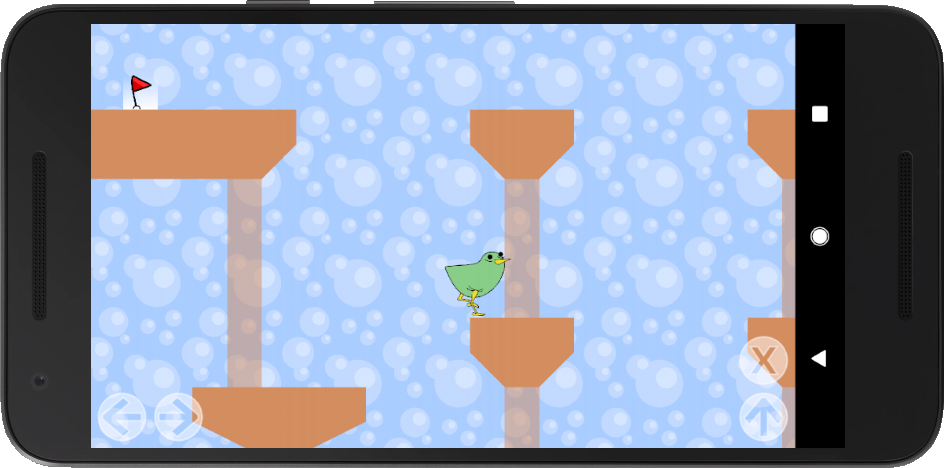
We have some kind of jump and run game, our character can walk left/right and jumping is possible as well. If we reach the red flag, the level is completed and a next level starts.
If we unpack the APK (APKs are just ZIP files, I used unzip flaggybird.apk) we can see that there are three zlib compressed levels inside the assets folder. I also noticed a small native library called library.so.
So far there is no clue about where the flag is hidden, and as the game is pretty hard (couldn’t reach level3) we need to get our hands dirty and start looking at the decompiled source.
Reversing
I used jadx for the decompilation of the app (jadx flaggybird.apk). Now, with the (mostly) recovered source, we can start investigation. The Checker.java file was chosen as an interesting startpoint, as it contained AES decoding routines:
class Checker {
private static final byte[] a = new byte[]{(byte) 46, (byte) 50, ...};
private static final byte[] b = new byte[]{(byte) -30, (byte) 1, ...};
private static final byte[] c = new byte[]{(byte) -113, (byte) -47, ...};
private byte[] a(byte[] bArr, byte[] bArr2) {
try {
IvParameterSpec ivParameterSpec = new IvParameterSpec(b);
SecretKeySpec secretKeySpec = new SecretKeySpec(bArr, "AES");
Cipher instance = Cipher.getInstance("AES/CBC/PKCS5PADDING");
instance.init(2, secretKeySpec, ivParameterSpec);
return instance.doFinal(bArr2);
} catch (Exception unused) {
return null;
}
}
public byte[] a(byte[] bArr) {
if (nativeCheck(bArr)) {
try {
if (Arrays.equals(MessageDigest.getInstance("SHA-256").digest(bArr), a)) {
return a(bArr, c);
}
} catch (Exception unused) {
}
}
return null;
}
public native boolean nativeCheck(byte[] bArr);
}
Array a is a sha256 sum, b the IV and c contains encrypted data. We can see that if the native nativeCheck returns true for some bArr, it’s sha256 is compared against a.
Only if they match, decryption takes place. So we are looking for a decryption key with the sha256 sum of a. To find the decryption key, we need to find out where bArr comes from and what nativeCheck does.
Eggs And Arrays
The only occurrence of the Checker class is in f.java. There are two interesting methods in this file and a lot of enums.
class f {
static final a[] a = new a[]{a.EGG_0, a.EGG_1, ..., a.EGG_15};
...
public void a() {
byte[] bArr = new byte[32];
for (int i = 0; i < this.l.length; i++) {
for (int i2 = 0; i2 < a.length; i2++) {
if (this.l[i] == a[i2]) {
bArr[i] = (byte) i2;
}
}
}
bArr = new Checker().a(bArr);
if (bArr != null) {
try {
this.o = 0;
a(bArr);
return;
} catch (IOException unused) {
return;
}
}
this.g.a("Close, but no cigar.");
}
This method is responsible for calling the Checker. Before it does so, it constructs the bArr. The construction looks quite messy, but it just translates enum elements (like a.EGG_0, etc) into a numerical representation.
In our case EGG_0 is translated to 0, EGG_1 to 1, etc. Therefore the real “array of interest” for us is l. But what we know so far is, that the bytevalues for bArr are all in the range [0-15], as the a array only contains 16 eggs.
public void a(int i, int i2) {
this.l[i] = a[i2];
int i3 = -1;
for (int i4 = 0; i4 < this.m.size(); i4++) {
if (((Integer) this.m.get(i4)).intValue() == i) {
if (i2 == 0) {
i3 = i4;
} else {
return;
}
}
}
if (i3 != -1) {
this.m.remove(i3);
}
if (i2 != 0) {
this.m.add(Integer.valueOf(i));
if (this.m.size() > 15) {
this.l[((Integer) this.m.remove(0)).intValue()] = a.EGG_0;
}
}
}
This function is called to modify elements of l. It assigns l at position i the value of i2 (as an “EGG_*” enum value, but translated back anyways later as we could see).
Also, in the remaining part of the method, it is ensured that there are no more than 15 nonzero eggs inside the l array and that every egg only occurs once! This reduces the possible keyspace further. For example the following keys would be possible:
[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]
[3,0,11,0,10,8,0,0,13,1,0,0,12,0,6,9,5,0,0,2,7,0,0,0,0,0,14,0,15,0,4,0]
At this point I stopped the java reversing part.
NativeCheck
I started with throwing library.so into IDAs / ghidras decompiler. I used the ARM library version, as they tend to produce better decompilation results.
bool C(char *bArr)
{
int v1;
bool result;
unsigned char v4[16];
v1 = 0;
do {
v4[v1] = bArr[2 * v1] + bArr[2 * v1 + 1];
++v1;
} while ( v1 != 16 );
p = 0;
c = 1;
M(v4, 16);
return v4[15] < 16 && c != 0;
}
After some Java unwrapping C is called. bArr is compressed down to 16 Bytes by summing up two adjacent bytes, e.g. [x1, x2, x3, x4, …, x32] -> [x1 + x2, x3 + x4, …, x31 + x32]. Afterwards M is called. Apparently the goal is to keep c == 1 during the execution of M.
Also, we get another constraint for the possible keyspace with x31 + x32 < 16.
Now we get to the main part of the nativeCheck. It is some recursive algorithm which I didn’t bother to look at so closely. The only depency is a boolean array.
Straight outta IDA:
int c = 1;
int p = 0;
int d[] = {0x00000000U, 0x00000000U, 0x00000000U, 0x00000000U, 0x00000001U,
0x00000000U, 0x00000000U, 0x00000001U, 0x00000000U, 0x00000001U,
0x00000001U, 0x00000001U, 0x00000001U, 0x00000000U, 0x00000000U,
0x00000000U, 0x00000001U, 0x00000001U, 0x00000000U, 0x00000000U,
0x00000001U, 0x00000000U, 0x00000001U, 0x00000000U, 0x00000000U,
0x00000000U, 0x00000001U, 0x00000001U, 0x00000001U, 0x00000000U,
0x00000000U, 0x00000000U, 0x00000001U, 0x00000000U, 0x00000000U,
0x00000000U, 0x00000000U, 0x00000001U, 0x00000001U, 0x00000001U,
0x00000001U, 0x00000001U, 0x00000000U, 0x00000001U, 0x00000000U,
0x00000000U, 0x00000000U};
void M(char *dest, int len) {
size_t middle; // r13
int halflen; // er12
char *middleptr; // rbp
size_t v5; // rbx
int v6; // er14
signed int v7; // eax
char v8; // dl
size_t v9; // rbp
char desta[16]; // [rsp+10h] [rbp-48h]
size_t v12; // [rsp+20h] [rbp-38h]
if (len >= 2) {
middle = len >> 1;
M(dest, len >> 1);
if (c) {
halflen = len - middle;
middleptr = &dest[middle];
M(&dest[middle], len - middle);
if (c) {
if (halflen > 0) {
v5 = 0LL;
v6 = 0;
v7 = 0;
while (1) {
v8 = middleptr[v6];
if (dest[v7] >= v8) {
if (dest[v7] <= v8 || d[p]) {
c = 0;
return;
}
++p;
desta[v5] = middleptr[v6++];
} else {
if (d[p] != 1) {
c = 0;
return;
}
++p;
desta[v5] = dest[v7++];
}
++v5;
if (v7 >= (signed int) middle || v6 >= halflen)
goto LABEL_17;
}
}
v7 = 0;
v6 = 0;
v5 = 0;
LABEL_17:
if (v7 < (signed int) middle) {
v9 = (unsigned int) (middle - 1 - v7);
memcpy(&desta[(signed int) v5], &dest[v7], v9 + 1);
v5 = v5 + v9 + 1;
}
if (v6 < halflen) {
memcpy(&desta[(signed int) v5], &dest[middle + v6], (unsigned int) (len - 1 - v6 - middle) + 1LL);
}
memcpy(dest, desta, len);
}
}
}
}
Solving
As it always takes some time for me to decompile algorithms properly (even tough this looked like a simple one) I decided just to write some small harness and use angr to compute a valid input array for M.
The harness:
int main(int argc, char* argv[]) {
char buf[16];
read(0, buf, 16);
M(buf, 16);
if (c)
puts("YAY!");
return 0;
}
The handy part about doing it this way is, that we only need to define our constraints. I used the following:
- Last byte of compressed key < 16 (because of the check in
C) - A single byte must be < 30 (14 + 15 = 29 maximum possible value for a byte)
- Summed up, all bytes must equal 120 (1+2+3+…+15 = 120)
The constraints from above still do allow for a few values we could have ruled out, but I just tried to keep them simple.
import angr
import claripy
if __name__ == '__main__':
p = angr.Project('./main', load_options={'auto_load_libs': False})
sym = claripy.BVS('x', 16 * 8)
state = p.factory.entry_state(args=[p.filename], stdin=sym)
state.add_constraints(sym.get_byte(15) < 16)
for i in range(15):
state.add_constraints(sym.get_byte(i) < 30)
state.add_constraints(sum([sym.get_byte(x) for x in range(16)]) == 120)
ex = p.factory.simulation_manager(state)
ex.explore(find=lambda s: b"YAY!" in s.posix.dumps(1))
f = ex.found[0].solver.eval(sym, cast_to=bytes)
print(list(f))
After less than 15 seconds we get a solution. It is also the only possible solution.
[9, 8, 7, 2, 11, 15, 13, 10, 6, 5, 14, 4, 3, 0, 12, 1]
Now we know the summed up key which M expects. Bruteforcing all possible values and comparing their hashes against the known hash should now be feasible. However I just used Z3 because I didn’t want to write a bruteforcer.
The first constraints are the problem definition. The second one requires the key to contain exactly 15 nonzero values.
Now we only have to loop until we find our key with the correct hash, constantly adding constraints to exclude already found, non-matching keys.
import hashlib
from z3 import *
arr = [9, 8, 7, 2, 11, 15, 13, 10, 6, 5, 14, 4, 3, 0, 12, 1]
correcthash = "2e325c91c914"
s = Solver()
vec = [BitVec('x{}'.format(x), 4) for x in range(32)]
for i in range(16):
s.add(vec[i * 2] + vec[i * 2 + 1] == arr[i])
s.add(sum([If(vec[i] != 0, 1, 0) for i in range(32)]) == 15)
while s.check() == sat:
x = s.model()
ress = [x[v].as_long() for v in vec]
s.add(Or([vec[i] != ress[i] for i in range(32)]))
h = hashlib.sha256()
h.update(bytes(ress))
if h.hexdigest().startswith(correcthash):
print(h.hexdigest())
print(ress)
In less than 2 minutes I obtained the decryption key.
[9, 0, 0, 8, 0, 7, 2, 0, 0, 11, 0, 15, 13, 0, 10, 0, 6, 0, 0, 5, 14, 0, 0, 4, 0, 3, 0, 0, 12, 0, 1, 0]
After decryption we get a zlib compressed level file. I couldn’t tell the flag from the decompressed content, so I just replaced the first level with it. Then resigning the APK with jarsigner finally leads us to the flag.
