VolgaCTF Quals 2018 - Forbidden

The Task came with the description:

Our friend tried to send us all his BTCs, but MAC of the transaction was lost. 
We need your help to compute MAC for this encrypted transaction.

Send it in format VolgaCTF{AuthTag_in_HEX}.

And the following Python code:

from cryptography.hazmat.backends import default_backend
from cryptography.hazmat.primitives.ciphers import (
    Cipher, algorithms, modes
)
from secret import key


def encrypt(iv, key, plaintext, associated_data):
    encryptor = Cipher(
        algorithms.AES(key),
        modes.GCM(iv),
        backend=default_backend()
    ).encryptor()
    encryptor.authenticate_additional_data(associated_data)
    ciphertext = encryptor.update(plaintext) + encryptor.finalize()

    return (ciphertext, encryptor.tag)


def decrypt(key, associated_data, iv, ciphertext, tag):
    decryptor = Cipher(
        algorithms.AES(key),
        modes.GCM(iv, tag),
        backend=default_backend()
    ).decryptor()
    decryptor.authenticate_additional_data(associated_data)

    return decryptor.update(ciphertext) + decryptor.finalize()


iv = "9313225df88406e555909c5aff5269aa".decode('hex')
key = key.decode('hex')

ciphertext1, tag1 = encrypt(iv, key, "From: John Doe\nTo: John Doe\nSend 100 BTC", "John Doe")
ciphertext2, tag2 = encrypt(iv, key, "From: VolgaCTF\nTo: VolgaCTF\nSend 0.1 BTC", "VolgaCTF")
ciphertext3, tag3 = encrypt(iv, key, "From: John Doe\nTo: VolgaCTF\nSend ALL BTC", "John Doe")

And the textfile:

(C1, T1) = (1761e540522379aab5ef05eabc98516fa47ae0c586026e9955fd551fe5b6ec37e636d9fd389285f3, 0674d6e42069a10f18375fc8876aa04d)
(C2, T2) = (1761e540522365aab1e644ed87bb516fa47ae0d9860667d852c6761fe5b6ec37e637c7fc389285f3, cf61b77c044a8fb1566352bd5dd2f69f)
C3 = 1761e540522379aab5ef05eabc98516fa47ae0d9860667d852c6761fe5b6ec37e646a581389285f3

The encrypt function does an authenticated encryption of a plaintext and associated data using AES in Galois/Counter Mode(GCM).

The function outputs a tuple containing the ciphertext and a GCM authentication tag. The authentication tag guarantees that the ciphertext and the associated data (which is not encrypted) have not been tampered with.

So the task here is to forge a valid tag under an unknown key for the plaintext P3: From: John Doe\nTo: VolgaCTF\nSend ALL BTC with the associated data A3: John Doe. We have two valid ciphertext/tag pairs and the ciphertext of P3 to do so.

The cryptography Python module uses the supplied IV as nonce in the Counter Mode AES. The code shows that the same IV/nonce was used for all encryptions!

This is of course a very bad idea, and - as it turns out - two ciphertext/tag tuples together with their associated data is enough to forge authentication tags. Note that all these values are public in real encryption systems using GCM.

The calculation of the authentication tag in GCM can be seen in this graph:

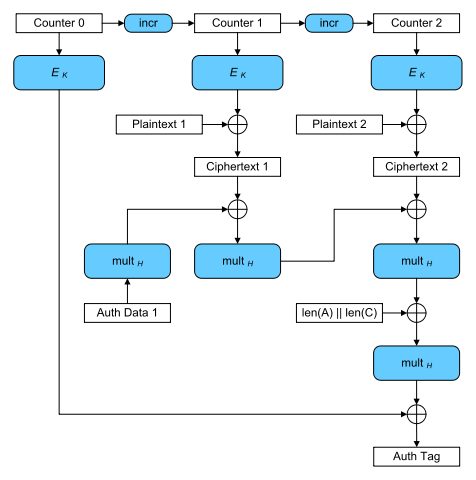
H is the hash key calculated by the encryption of a zero block under the encryption key $H = E_k(0)$. $Gmul_H(X)$ denotes the multiplication with H in the Galois Field $GF(2^{128})$.

To forge an authentication tag we employ the forbidden attack. The attack works if a nonce was illegally used multiple times (hence the name). It is described (a.o.) here.

So how does the attack work? The calculation of the authentication tag can also be viewed as a polynomial:

$g(X) = A_1X^{m+n+1} + ... + A_mX^{n+2} + C_1X^{n+1} + C_nX^2 + LX + E_k(J_0)$

The authentication tag $T$ can then be calculated as $g(H) = T$.

The coefficients $A_i$ and $C_i$, denote the associated data blocks and ciphertext blocks. $L$ denotes the length of the whole message and $E_k(J_0)$ a nonce derived value. All of the coefficients are 128 bit long blocks used as binary polynomials in $GF(2^{128})$.

In our case, the polynomials used to create the known tags have the form:

$f_1(X) = A_{1,1}X^{5} + C_{1,1}X^{4} + C_{1,2}X^3 + C_{1,3}X^2 + LX + E_k(J_0)$ $f_2(X) = A_{2,1}X^{5} + C_{2,1}X^{4} + C_{2,2}X^3 + C_{2,3}X^2 + LX + E_k(J_0)$

With the same amount of associated data and ciphertext blocks as well as identical $E_k(J_0)$ and $L$. Evaluating these polynomials at H (the hash key) would give us the corresponding authentication tag $f_1(H) = T_1$. If we now deduct the tags from the polynomials:

$f'_1(X) = A_{1,1}X^{5} + C_{1,1}X^{4} + C_{1,2}X^3 + C_{1,3}X^2 + LX + E_k(J_0) + T_1$ $f'_2(X) = A_{2,1}X^{5} + C_{2,1}X^{4} + C_{2,2}X^3 + C_{2,3}X^2 + LX + E_k(J_0) + T_2$

we get polynomials that evaluate to 0 at H: $f'_1(H) = 0$, making the hash key H a root of both. Every coefficient in these polynomial is known except for $E_k(J_0)$, which is identical in both polynomials since the nonce was reused. So if we substract them from each other (note that adding and substracting is the same in $GF(2^{128})$):

$g(X) = f'_1(X) + f'_2(X)$

we get a polynomial with known coefficients and H as a root:

$g(X) = (A_{1,1} + A_{2,1})X^{5} + (C_{1,1} + C_{2,1})X^{4} + ... + LX + T_1 + T2$

The roots of this polinomial are candidates for the hash key H. Since we work in $GF(2^{128})$ adding the coefficients is the same as XORing their respective blocks.

Now we can calculate the missing $E_k(J_0)$ by evaluating:

$E_k(J_0) = f'_1(H) + A_{1,1}H^{5} + C_{1,1}H^{4} + C_{1,2}H^3 + C_{1,3}H^2 + LH + T_1$

By putting all this together we can finally calculate the authentication tag for message 3. Since we know the ciphertext C3 as well aus the associated data A3 we just have to plug it in:

$f_3(H) = A_{3,1}H^{5} + C_{3,1}H^{4} + C_{3,2}H^3 + C_{3,3}H^2 + LH + E_k(J_0)$

The final exploit gives us two possible flags, one per root:

$sage -python forb_expl.py
VolgaCTF{B084B54CB9D114C6912926F4EC42DBCF}
VolgaCTF{2AA1B52883378169C96072EA74BB41A1}

Turns out VolgaCTF{B084B54CB9D114C6912926F4EC42DBCF} was correct \o/.

Credits for this task actually go to my collegue chemmi who solved the task before me!