SIDHE

Sidhe was a post-quatum crypto task of this year’s PlaidCTF.

The Vulnerable Server

We’re given network access to a server and it’s source code:

import hashlib
from Crypto.Cipher import AES
import sys
assert(sys.version_info.major >= 3)

# SIDH parameters from SIKEp434
# using built-in weierstrass curves instead of montgomery curves because i'm lazy
e2 = 0xD8
e3 = 0x89
p = (2^e2)*(3^e3)-1
K.<ii> = GF(p^2, modulus=x^2+1)
E = EllipticCurve(K, [0,6,0,1,0])
xP20 = 0x00003CCFC5E1F050030363E6920A0F7A4C6C71E63DE63A0E6475AF621995705F7C84500CB2BB61E950E19EAB8661D25C4A50ED279646CB48
xP21 = 0x0001AD1C1CAE7840EDDA6D8A924520F60E573D3B9DFAC6D189941CB22326D284A8816CC4249410FE80D68047D823C97D705246F869E3EA50
yP20 = 0x0001AB066B84949582E3F66688452B9255E72A017C45B148D719D9A63CDB7BE6F48C812E33B68161D5AB3A0A36906F04A6A6957E6F4FB2E0
yP21 = 0x0000FD87F67EA576CE97FF65BF9F4F7688C4C752DCE9F8BD2B36AD66E04249AAF8337C01E6E4E1A844267BA1A1887B433729E1DD90C7DD2F
xQ20 = 0x0000C7461738340EFCF09CE388F666EB38F7F3AFD42DC0B664D9F461F31AA2EDC6B4AB71BD42F4D7C058E13F64B237EF7DDD2ABC0DEB0C6C
xQ21 = 0x000025DE37157F50D75D320DD0682AB4A67E471586FBC2D31AA32E6957FA2B2614C4CD40A1E27283EAAF4272AE517847197432E2D61C85F5
yQ20 = 0x0001D407B70B01E4AEE172EDF491F4EF32144F03F5E054CEF9FDE5A35EFA3642A11817905ED0D4F193F31124264924A5F64EFE14B6EC97E5
yQ21 = 0x0000E7DEC8C32F50A4E735A839DCDB89FE0763A184C525F7B7D0EBC0E84E9D83E9AC53A572A25D19E1464B509D97272AE761657B4765B3D6
xP30 = 0x00008664865EA7D816F03B31E223C26D406A2C6CD0C3D667466056AAE85895EC37368BFC009DFAFCB3D97E639F65E9E45F46573B0637B7A9
xP31 = 0x00000000
yP30 = 0x00006AE515593E73976091978DFBD70BDA0DD6BCAEEBFDD4FB1E748DDD9ED3FDCF679726C67A3B2CC12B39805B32B612E058A4280764443B
yP31 = 0x00000000
xQ30 = 0x00012E84D7652558E694BF84C1FBDAAF99B83B4266C32EC65B10457BCAF94C63EB063681E8B1E7398C0B241C19B9665FDB9E1406DA3D3846
xQ31 = 0x00000000
yQ30 = 0x00000000
yQ31 = 0x0000EBAAA6C731271673BEECE467FD5ED9CC29AB564BDED7BDEAA86DD1E0FDDF399EDCC9B49C829EF53C7D7A35C3A0745D73C424FB4A5FD2
P2 = E(xP20+ii*xP21, yP20+ii*yP21)
Q2 = E(xQ20+ii*xQ21, yQ20+ii*yQ21)
P3 = E(xP30+ii*xP31, yP30+ii*yP31)
Q3 = E(xQ30+ii*xQ31, yQ30+ii*yQ31)

def elem_to_coefficients(x):
    l = x.polynomial().list()
    l += [0]*(2-len(l))
    return l

def elem_to_bytes(x):
    n = ceil(log(p,2)/8)
    x0,x1 = elem_to_coefficients(x) # x == x0 + ii*x1
    x0 = ZZ(x0).digits(256, padto=n)
    x1 = ZZ(x1).digits(256, padto=n)
    return bytes(x0+x1)

def isogen3(sk3):
    Ei = E
    P = P2
    Q = Q2
    S = P3+sk3*Q3
    for i in range(e3):
        # Give generator of subgroup
        phi = Ei.isogeny((3^(e3-i-1))*S)
        # Ei = target curve of isogeny
        Ei = phi.codomain()
        # points on target curve
        S = phi(S)
        P = phi(P)
        Q = phi(Q)
    return (Ei,P,Q)

def isoex3(sk3, pk2):
    Ei, P, Q = pk2
    S = P+sk3*Q
    for i in range(e3):
        R = (3^(e3-i-1))*S
        phi = Ei.isogeny(R)
        Ei = phi.codomain()
        S = phi(S)
    return Ei.j_invariant()

def recv_K_elem(prompt):
    print(prompt)
    re = ZZ(input("  re: "))
    im = ZZ(input("  im: "))
    return K(re + ii*im)

supersingular_cache = set()
def is_supersingular(Ei):
    a = Ei.a_invariants()
    if a in supersingular_cache:
        return True
    result = Ei.is_supersingular(proof=False)
    if result:
        supersingular_cache.add(a)
    return result

def recv_and_validate_pk2():
    print("input your public key:")
    a1 = recv_K_elem("a1: ")
    a2 = recv_K_elem("a2: ")
    a3 = recv_K_elem("a3: ")
    a4 = recv_K_elem("a4: ")
    a6 = recv_K_elem("a6: ")
    Ei = EllipticCurve(K, [a1,a2,a3,a4,a6])
    assert(is_supersingular(Ei))
    Px = recv_K_elem("Px: ")
    Py = recv_K_elem("Py: ")
    P = Ei(Px, Py)
    Qx = recv_K_elem("Qx: ")
    Qy = recv_K_elem("Qy: ")
    Q = Ei(Qx, Qy)
    assert(P*(3^e3) == Ei(0) and P*(3^(e3-1)) != Ei(0))
    assert(Q*(3^e3) == Ei(0) and Q*(3^(e3-1)) != Ei(0))
    assert(P.weil_pairing(Q, 3^e3) == (P3.weil_pairing(Q3, 3^e3))^(2^e2))
    return (Ei, P, Q)

def main():
    sk3 = randint(1,3^e3-1)
    pk3 = isogen3(sk3)
    print("public key:")
    print("a1:", elem_to_coefficients(pk3[0].a1()))
    print("a2:", elem_to_coefficients(pk3[0].a2()))
    print("a3:", elem_to_coefficients(pk3[0].a3()))
    print("a4:", elem_to_coefficients(pk3[0].a4()))
    print("a6:", elem_to_coefficients(pk3[0].a6()))
    print("Px:", elem_to_coefficients(pk3[1][0]))
    print("Py:", elem_to_coefficients(pk3[1][1]))
    print("Qx:", elem_to_coefficients(pk3[2][0]))
    print("Qy:", elem_to_coefficients(pk3[2][1]))
    super_secret_hash = hashlib.sha256(str(sk3).encode('ascii')).digest()[:16]

    for _ in range(300):
        try:
            # SIDH key exchange
            pk2 = recv_and_validate_pk2()
            shared = isoex3(sk3, pk2)
            key = hashlib.sha256(elem_to_bytes(shared)).digest()
            # test shared key
            cipher = AES.new(key, AES.MODE_ECB)
            ciphertext = input("ciphertext: ")
            plaintext = cipher.decrypt(bytes.fromhex(ciphertext))
            if plaintext == super_secret_hash:
                print("How did you find my secret? Here, have a flag:")
                with open("flag.txt","r") as f:
                    print(f.read())
                return
            elif plaintext == b"Hello world.\x00\x00\x00\x00":
                print("Good ciphertext.")
            else:
                print("Bad ciphertext!")
        except:
            print("Validation error!")
            return

if __name__ == '__main__':
    main()

This code implements a Supersingular isogeny Diffie–Hellman key exchange (SIDH), specifically the De Feo, Jao, and Plut Scheme. This is a post-quantum key exchange mechanism based on graphs of isogenies $\phi$ (the edges) between supersingular elliptic curves $E$ (the vertices). The goal here is to recover the private key of the server.

The code reuses the private key portion sk3 up to 300 times. Also, it offers an oracle to determine if a shared key is valid, by decrypting a user suplied ciphertext. It also includes validation logic using the Weil pairing assert(P.weil_pairing(Q, 3^e3) == (P3.weil_pairing(Q3, 3^e3))^(2^e2)) to check independece of the supplied points by verfying their order.

In this scheme, Alice chooses a large random number $\alpha$ as private key. Then she calculates an isogeny $\phi_a$ from this number and two predefined points $P_A$ , $P_B$ in the $E[2^n]$ torsion group of the scheme’s supersingular elliptic curve $E$ . She then sends the parameters $(E_A = \phi_A(E), \phi_A(P_B), \phi_A(Q_B))$ to Bob. Bob does essentially the same calculation, but in $E[3^n]$ . Once Alice receives Bob’s parameters $(E_B = \phi_B(E), \phi_B(P_A), \phi_B(Q_A))$ , she can calculate the isogeny from $E_B$ by using her private key $\phi_B(P_A) + \alpha \phi_B(Q_A)$ .

The scheme is illustrated in this graph (taken from the original publication):

SIDH

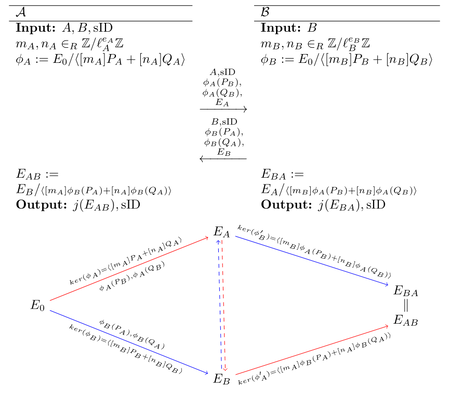
Static SIDH Attack

Reusing private keys in Diffie Hellman is a common use case, called static DH. With SIDH however, it is a very bad idea to use non-ephemeral keys. Since we have an oracle that tells us if a shared key is correct or not, we can employ an adaptive attack to recover the private key bit-by-bit (or actually trit-by-trit here).

As you can see in the code, the j-invariant is used as the shared key return Ei.j_invariant(). That is because the scheme guarantees that both parties end up on isomprphic curves, but not neccessarily on the same curve. The trick behind this attack is to calculate a legitimate isogeny giving $(E_B = \phi_B(E), R=\phi_B(P_A), S=\phi_B(Q_A))$ and doing the key exchange as Bob. Now we received a shared key in the form of a j-invariant of the agreed upon curve isomphism class. To recover the first bit of Alice’s private key we’ll then supply the values $(E_B = \phi_B(E), R, S+2^{n-1}R)$ . Alice (the server) will now compute $R + \alpha (S+2^{n-1}R)$ and calculate a shared key based on the result. Since $R$ has order $2^n$ , it holds that $\alpha (S+2^{n-1}R) = S$ iff $\alpha$ is even, because then:

$\alpha S + \frac{\alpha}{2} \cdot 2 \cdot 2^{n-1}R = \alpha S + \frac{\alpha}{2} \cdot 2^{n}R = \alpha S+ \frac{\alpha}{2} \cdot 0 = \alpha S$

So only if alpha is even, the shared key will be equal to the original (legitimate) one. Because of this, we just recovered the lowest bit of Alice’s private key. With the same trick we can recover all bits of the private key. For mathematical background information of the attack see this paper on insecurities of SIDH. To bypass the check via Weil pairing we need to include a scaling factor $\theta$ . However, that is not possible for the highest bits. We therefore have to brute force a hand-ful of bits offline, which is not a problem.

Exploit

The given server code does the computation on $E[3^n]$ , so it is actually playing Bob not Alice. However, the Static SIDH attack works exactly the same. The only difference is that we view the server key in trits instead of bits: $\alpha= \alpha_0 + \alpha_1\cdot3^1 + \ldots + \alpha_i\cdot3^i$ . Since a trit can have three possible values instead of two, we need to query the oracle more often per ‘position’. An that’s all!

A full exploit script (by manf since he was faster than me :/) can be found here.